
 ��ͼ��������ABCD�У�AB=6����ABC=60�㣬����E��Fͬʱ�ӵ�B���������е�E�ӵ�B���A��ÿ��1����λ���ٶ��˶�����F�ӵ�B������B-C-A��·�����յ���ÿ��2����λ���ٶ��˶�����EFΪ�����ϣ������ң����ȱ�������EFG��AH�ǡ�ABC��BC���ϵĸߣ������˶�ʱ��Ϊt�룬��EFG�͡�AHC���غϲ���ʱ���غϲ���ͼ�ε��ܳ�ΪL��
��ͼ��������ABCD�У�AB=6����ABC=60�㣬����E��Fͬʱ�ӵ�B���������е�E�ӵ�B���A��ÿ��1����λ���ٶ��˶�����F�ӵ�B������B-C-A��·�����յ���ÿ��2����λ���ٶ��˶�����EFΪ�����ϣ������ң����ȱ�������EFG��AH�ǡ�ABC��BC���ϵĸߣ������˶�ʱ��Ϊt�룬��EFG�͡�AHC���غϲ���ʱ���غϲ���ͼ�ε��ܳ�ΪL������ ��1�������ε����ʵó�BC=AB=6�ó�CF=BC-BF=6-2t���ɣ�
��2�������ε����ʺ���֪�����ó���ABC�ǵȱ������Σ��ó���ACB=60�㣬�ɵȱ������ε����ʺ����Ǻ����ó���GEF=60�㣬GF=EF=BF•sin60��=$\sqrt{3}$t��֤����GFC=90�㣬�����Ǻ������CF=$\frac{GF}{tan60��}$=t����BF+CF=BC�ó����̣��ⷽ�̼��ɣ�
��3��������������ٵ�$\frac{3}{2}$��t��2ʱ���������ε��ܳ���ʽ���ɵó�������ڵ�2��t��3ʱ���ɢٵĽ�����ó����ۣ��۵�3��t��6ʱ���ɢٵĽ�����ó����ۣ�
���  �⣺��1����������ã�BF=2t��
�⣺��1����������ã�BF=2t��
���ı���ABCD�����Σ�
��BC=AB=6��
�൱0��t��6ʱ��CF=BC-BF=6-2t��
��6��t��12ʱ��CF=2t-6��
��2����G�����߶�AC��ʱ����ͼ1��ʾ��
���ı���ABCD�����Σ�
��AB=BC��
�ߡ�ABC=60�㣬
���ABC�ǵȱ������Σ�
���ACB=60�㣬
�ߡ�EFG�ǵȱ������Σ�
���GFE=60�㣬GF=EF=BF•sin60��=$\sqrt{3}$t��
��EF��AB��
���BFE=90��-60��=30�㣬
���GFB=90�㣬
���GFC=90�㣬
��CF=$\frac{GR}{tan60��}$=$\frac{\sqrt{3}t}{\sqrt{3}}$=t��
��BF+CF=BC��
��2t+t=6��
��ã�t=2��
��3����$\frac{3}{2}$��t��2ʱ����ͼ2��L=2$\sqrt{3}$t+$\frac{2}{\sqrt{3}}$��2t-3��=$\frac{10}{3}\sqrt{3}t$-2$\sqrt{3}$��
��2��t��3ʱ����ͼ3��ʾ��L=$\sqrt{3}$t+$\frac{1}{2}$��6-t����$\frac{\sqrt{3}}{3}$+[6-$\frac{1}{2}$��6-t��-2��6-2t��]+$\sqrt{3}$��6-2t��=$\frac{27-7\sqrt{3}}{6}t$+7$\sqrt{3}$-9��
��3��t��6ʱ����ͼ4��L=$\sqrt{3}$��6-t��+$\frac{\sqrt{3}}{2}$��$\sqrt{3}$��6-t��+$\frac{1}{2}$��6-t����$\frac{\sqrt{3}}{3}$=-$\frac{7\sqrt{3}+9}{6}t$+7$\sqrt{3}$+9��
���� �������ı����ۺ���Ŀ�����������ε����ʡ��ȱ������ε��ж������ʡ����Ǻ���������������ļ����֪ʶ�������ۺ���ǿ���ѶȽϴ��ر��ǣ�3���У���Ҫ���з������۲��ܵó������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 1 | C�� | -1 | D�� | -7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 2.2 | C�� | 2.4 | D�� | 2.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 12 | C�� | 24 | D�� | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
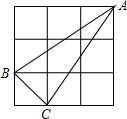 ��ͼ���������������У�ÿ��С�����εı߳���Ϊ1����ABC������������ڸ���ϣ����ABC�����Ϊ$\frac{5}{2}$��
��ͼ���������������У�ÿ��С�����εı߳���Ϊ1����ABC������������ڸ���ϣ����ABC�����Ϊ$\frac{5}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 3 | B�� | 4 | C�� | 2$\sqrt{2}$-1 | D�� | 6$\sqrt{2}$-6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У�E��F�ֱ���BC��CD���е㣬����AE��BF����G������ABE�Ƶ�A��ʱ�뷽����ת��ʹ��AB��������AE�ϣ����õ���AHM��AM��BF�ཻ�ڵ�N����������ABCD�����Ϊ4ʱ�����ı���GHMN�����Ϊ$\frac{1}{5}$��
��ͼ��������ABCD�У�E��F�ֱ���BC��CD���е㣬����AE��BF����G������ABE�Ƶ�A��ʱ�뷽����ת��ʹ��AB��������AE�ϣ����õ���AHM��AM��BF�ཻ�ڵ�N����������ABCD�����Ϊ4ʱ�����ı���GHMN�����Ϊ$\frac{1}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABC�Ƶ�A��ת����ADE��λ�ã�ʹ��D�䵽�߶�AB�Ĵ�ֱƽ�����ϣ�����ת�ǵĶ���Ϊ��������
��ͼ������ABC�Ƶ�A��ת����ADE��λ�ã�ʹ��D�䵽�߶�AB�Ĵ�ֱƽ�����ϣ�����ת�ǵĶ���Ϊ��������| A�� | 40�� | B�� | 50�� | C�� | 60�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�ÿ��С�����εĶ���и�㣬��ABC�Ķ�����ڸ���ϣ�O��MҲ�ڸ���ϣ�
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�ÿ��С�����εĶ���и�㣬��ABC�Ķ�����ڸ���ϣ�O��MҲ�ڸ���ϣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com