
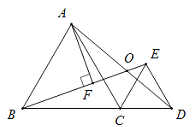
【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】C
【解析】
根据等边三角形的性质易证△BCE≌△ACD,根据全等三角形的性质可得∠CBE=∠CAD,再根据三角形外角的性质求得∠BOD=120°,即可求得∠AOF=60°,在Rt△AOF中,∠AOF=60°,OF=1,即可求得AF=![]() .
.
∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中, ,
,
∴△BCE≌△ACD(SAS)
∴∠CBE=∠CAD,
∵∠BOD=∠ABE+∠BAD,∠ABC=∠BAC=60°,
∴∠BOD=∠ABE+∠BAC+∠CAD=∠ABE+∠BAC+∠CBE=∠ABC+∠BAC=60°+60°=120°.
∴∠AOF=180°-∠BOD=180°-120°=60°,
在Rt△AOF中,∠AOF=60°,OF=1,
∴AF=![]() .
.
故答案为:![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,客轮沿折线A—B—C从A点出发经过B点再到C点匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批货物送达客轮,两船同时起航,并同时到达折线A—B—C上的某点E处,已知AB=BC=200海里,∠ABC=90°,客轮的速度是货轮速度的2倍.
(1)选择题:两船相遇之处E点( )
A.在线段AB上
B.在线段BC上
C.可能在线段AB上,也可能在线段BC上
(2)货轮从出发到两船相遇共航行了多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元.
(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任拿出200元学校奖励基金交给小芳,再次购买上述价格的钢笔和笔记本共48件作为奖品,奖励给校运动会中表现突出的同学,经双方协商,商店给出优惠是购买商品的总金额超出50的部分给打九折,请问小芳至少要买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
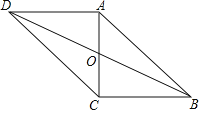
【题目】如图,在ABCD中,对角线AC、BD交于点O,AC⊥BC,且ABCD的周长为36,△OCD的周长比△OBC的周长大2.
(1)求BC,CD的长;
(2)求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).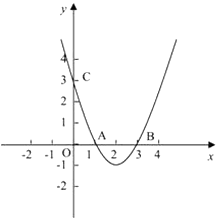
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,∠B=∠C,要使四边形ABCD为矩形,还需添加一个条件,这个条件可以是( )
A. AB=CD
B. AC=BD
C. ∠A=∠D
D. ∠A=∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图1,先把正方形ABCD对折,折痕为MN.
第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.
(1)判断△PBC的形状,并说明理由;
(2)作点C关于直线AP的对称点C′,连接PC′、DC′.
①在图2中补全图形,并求出∠APC′的度数;
②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)
查看答案和解析>>
科目:初中数学 来源: 题型:
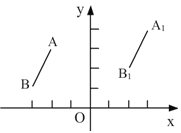
【题目】如图,在平面直角坐标系中,线段![]() 是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若
是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若![]() 的坐标为(3,4).
的坐标为(3,4).
(1)![]() 的坐标为 ;
的坐标为 ;
(2)若线段AB上一点P的坐标为(![]() ,
,![]() ),则点P的对应点
),则点P的对应点![]() 的坐标 .
的坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com