�Ķ�������ϣ���������и��⣺
������a
b=N��ʽ���У������Ѿ��о������������
����֪a��b����N�����dz˷����㣻
����֪b��N����a�����ǿ������㣻
���������о��������������֪a��N����b�����ǰ�������������������㣮
���壺���a
b=N��a��0��a��1��N��0������b������aΪ��N�Ķ���������b=log
aN��
���磺��Ϊ2
3=8������log
28=3����Ϊ
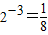
������
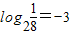
��
��1�����ݶ�����㣺
��log
381=______����log
33=______����log
31=______��
�����log
x16=4����ôx=______��
��2����a
x=M��a
y=N����log
aM=x��log
aN=y��a��0��a��1��M��N����������
��a
x•a
y=a
x+y����a
x+y=M•N��log
aMN=x+y��
��log
aMN=log
aM+log
aN
���Ƕ����������Ҫ����֮һ����һ�������ǻ����Եó���
log
aM
1M
2M
3��M
n=______������M
1��M
2��M
3������M
n��������a��0��a��1��
log
a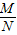
=______��a��0��a��1��M��N����������

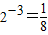 ������
������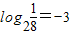 ��
��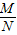 =______��a��0��a��1��M��N����������
=______��a��0��a��1��M��N����������

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
 ��
�� ��
�� .
. �Ľ�� ��
�Ľ�� �� = ����ʱ��
= ����ʱ�� ��
��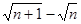 ��Ϊ��������ʽ��
��Ϊ��������ʽ��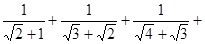 ��+
��+  ��
��