
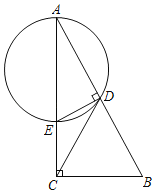
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD为斜边AB的中线.过点D作AB的垂线交AC于点E,再过A、D、E三点作⊙O.
(1)确定⊙O的圆心O的位置,并证明CD为⊙O的切线;
(2)若BC=3,求⊙O的直径.
【答案】(1)圆心O在AE的中点处,见解析;(2)2![]()
【解析】
(1)求出∠ADE=90°,根据圆周角定理求出AE为直径,即可得出答案;求出OD⊥DC,根据切线的判定得出即可;
(2)解直角三角形求出AB,求出AD,解直角三角形求出AE即可.
(1)解:∵点D在⊙O上,DE⊥AB,
∴∠ADE=90°,
∴AE为⊙O的直径,
∴圆心O在AE的中点处;
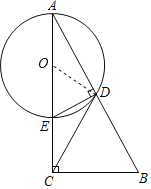
证明:连接OD,
∵∠A=30°,
∴∠COD=2∠A=60°,
∵在Rt△ACB中,CD为斜边AB上的中线,
∴CD=![]() AB=AD,
AB=AD,
∴∠OCD=∠A=30°,
∴∠ODC=180°﹣60°﹣30°=90°,
即OD⊥DC,
∵OD过O,
∴CD为⊙O的切线;
(2)解:∵在Rt△ABC中,∠A=30°,BC=3,
∴AB=2BC=6,
∵D为AB的中点,
∴AD=BD=3,
在Rt△ADE中,AE=![]() =
=![]() =2
=2![]() ,
,
∴⊙O的直径为2![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,E为AB上一点,以AE为直径作⊙O与BC相切于点D,连接ED并延长交AC的延长线于点F.
(1)求证:AE=AF;
(2)若AE=5,AC=4,求BE的长.
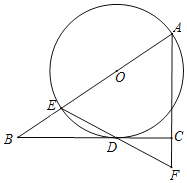
查看答案和解析>>
科目:初中数学 来源: 题型:
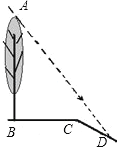
【题目】如图,坡面CD的坡比为![]() ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=![]() 米,则小树AB的高是 .
米,则小树AB的高是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段 AB 先向右平移 5 个单位,再将所得线段绕原点按顺时针方向旋转 90°,得到线段 AB ,则点 B 的对应点 B′的坐标是( )

A.(-4 , 1)B.( -1, 2)C.(4 ,- 1)D.(1 ,- 2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月18日,《感动中国2018年度人物颁奖盛典》在央视综合频道播出,其中乡村教师张玉滚的事迹令人非常感动某校团委组织“支援乡村教育,帮助教师张玉滚”的捐款活动,以下为九年级(1)班捐款情况:
捐款金额(元) | 5 | 10 | 20 | 50 |
人数(人) | 12 | 13 | 16 | 11 |
则这个班学生捐款金额的中位数和众数分别为( )
A.15,50B.20,20C.10,20D.20,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某路灯灯架示意图,其中点A表示电灯,AB和BC为灯架,l表示地面,已知AB=2m,BC=5.7m,∠ABC=110°,BC⊥l于点C,求电灯A与地面l的距离.(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
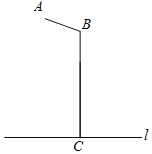
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学围绕“哈尔滨市周边五大名山,即:香炉山、凤凰山、金龙山、帽儿山、二龙山,你最喜欢那一座山?(每名学生必选且只选一座山)的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图的不完整的统计图:
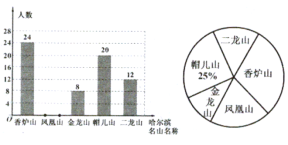
(1)求本次调查的样本容量;
(2)求本次调查中,最喜欢凤凰山的学生人数,并补全条形统计图;
(3)若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax![]() +bx+c的x,y的对应值如下表:
+bx+c的x,y的对应值如下表:
x | … | -1 |
| 0 |
| 1 |
| 2 | … |
y | … | -1 |
| m |
| 1 |
| n | … |
下列关于该函数性质的判断:①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com