
【题目】某地有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线 ![]() 与x轴相交于点A,与y轴相交于点B.
与x轴相交于点A,与y轴相交于点B.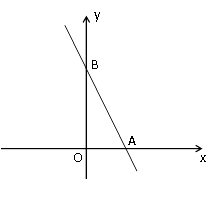
(1)直接写出A点的坐标;
(2)当x 时,y≤4;
(3)过B点作直线BP与x轴相交于P,若OP=2OA时,求ΔABP的面积。
(4)在y轴上是否存在E点,使得ΔABE为等腰三角形,若存在,直接写出满足条件的E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
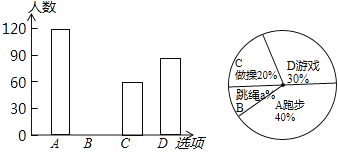
请结合统计图,回答下列问题:
(1)本次调查学生共 人,a= ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究函数y=x+![]() 的图象与性质】
的图象与性质】
(1)函数y=x+![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下列四个函数图象中函数y=x+![]() 的图象大致是 ;
的图象大致是 ;
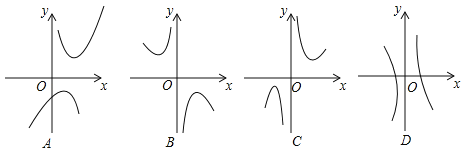
(3)对于函数y=x+![]() ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.
请将下列的求解过程补充完整.
解:∵x>0
∴y=x+![]() =(
=(![]() )2+(
)2+(![]() )2=(
)2=(![]() ﹣
﹣![]() )2+
)2+
∵(![]() ﹣
﹣![]() )2≥0
)2≥0
∴y≥ .
[拓展运用]
(4)若函数y=![]() ,则y的取值范围 .
,则y的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
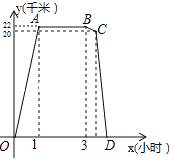
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式 | 批发 | 零售 | 储藏后销售 |
售价(元/吨) | 3000 | 4500 | 5500 |
成本(元/吨) | 700 | 1000 | 1200 |
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的 ![]() .
.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com