
 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).分析 (1)把P点坐标代入y=x+1可得b的值;
(2)根据方程组的解就是两函数图象的交点坐标可得答案;
(3)首先计算出直线l1与x轴的交点,再计算出直线l2的解析式,然后求出l2与x轴的交点,再求三角形的面积即可.
解答 解:(1)∵直线l1:y=x+1过点P(1,b),
∴b=1+1=2;
(2)∵点P(1,2),
∴方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(3)直线l1:y=x+1中当y=0时,x=-1,
∵直线l2:y=mx+n中n=3,
∴y=mx+3,
∵过P(1,2),
∴2=m+3,
解得:m=-1,
∴y=-x+3,
当y=0时,x=3,
∴直线l1、直线l2与y轴所围成的三角形的面积为:$\frac{1}{2}$×4×2=4.
点评 此题主要考查了一次函数与二元一次方程组,关键是掌握待定系数法求一次函数解析式,掌握凡是函数图象经过的点必能满足解析式即可.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
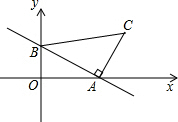 如图,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°
如图,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | S△COD=S△AOD | B. | S△ABC=S△ACD | C. | S△BOC=3•S△AOD | D. | S△BOC=9•S△AOD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 行驶时间(h) | 0 | 1 | 2 | 3 | 4 | 5 |
| 距乙地距离(km) | 800 | 720 | 640 | 560 | 480 | 400 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
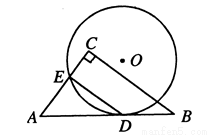
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2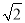 ,AC=3
,AC=3 ,BC=6,则⊙O的半径是__________________.
,BC=6,则⊙O的半径是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com