
设a1、a2、b1、b2都是实数,a1≠a2且(a1+b1)(a2+b2)=(a2+b1)(a1+b2)=1,求证:(a1+b1)(a2+b1)=(a1+b2)(a2+b2)=-1.
|
证明:按分析得到恒等式 (x+b1)(x+b2)-1=(x-a1)(x-a2). 令x=-b1,得 (-b1-a1)(-b1-a2)=-1 即(a1+b1)(a2+b1)=-1; 令x=-b2,得 (-b2-a1)(-b2-a2)=-1, 即(a1+b2)(a2+b2)=-1. 因此(a1+b1)(a2+b1)=(a1+b2)(a2+b2)=-1. 分析:用常规方法去做,繁琐、易错.仔细观察分析,发现已知条件的含义是二次方程(x+b1)(x+b2)=1有两个不相等的实数根x1=a1、x2=a2,与(x-a1)(x-a2)=0是同一个方程,于是有(x+b1)(x+b2)-1=(x-a1)(x-a2)恒成立,配凑出这个恒等式,取特殊值x=-b1,x=-b2便能证得结果. 说明:巧妙构造恒等式进行配凑,使证明过程变得简明、快捷. 由以上各例可以看出:巧妙进行配凑常能找到解决问题的捷径.同学们解题遇到困难,甚至一筹莫展时,不妨根据题目特点进行配凑尝试,或许能得到意外的惊喜. |


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
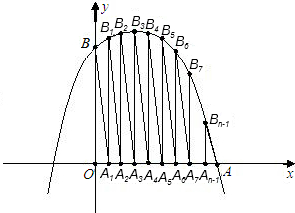 S2、S3、S4、…、Sn.
S2、S3、S4、…、Sn.查看答案和解析>>
科目:初中数学 来源: 题型:
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
| a1+a2+…+an |
| b1+b2+…+bn |
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 7 |
| 12 |
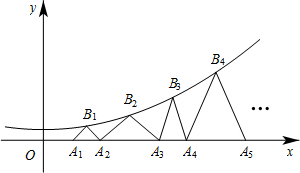
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com