【题目】为奖励优秀学生，某校准备购买一批文具袋和圆规作为奖品，已知购买1个文具袋和2个圆规需21元，购买2个文具袋和3个圆规需39元．
（1）求文具袋和圆规的单价．
（2）学校准备购买文具袋20个，圆规100个，文具店给出两种优惠方案：
方案一：每购买一个文具袋赠送1个圆规．
方案二：购买10个以上圆规时，超出10个的部分按原价的八折优惠，文具袋不打折．学校选择哪种方案更划算？请说明理由．
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案科目：初中数学 来源： 题型：
【题目】某汽车公司为了解某型号汽车在同一条件下的耗油情况，随机抽取了n辆该型号汽车耗油
所行使的路程作为样本，并绘制了以下不完整的频数分布直方图和扇形统计图．
根据题中已有信息，解答下列问题：
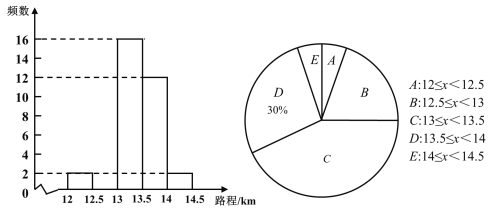
（1）求n的值，并补全频数分布直方图；
（2）若该汽车公司有600辆该型号汽车，试估计耗油所行使的路程低于
的该型号汽车的辆数；
（3）从被抽取的耗油所行使路程在
，
这两个范围内的4辆汽车中，任意抽取2辆，求抽取的2辆汽车来自同一范围的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，
的顶点A在反比例函数
的图像上，直线AB交y轴于点C，且点C的纵坐标为5，过点A、B分别作y轴的垂线AE、BF，垂足分别为点E、F，且
．
（1）若点E为线段OC的中点，求k的值；
（2）若为等腰直角三角形，
，其面积小于3．
①求证：
；
②把
称为
，
两点间的“ZJ距离”，记为
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，点P是平面内不与点A，C重合的任意一点，连接
，将线段绕点P旋转
得到线段
，连结
．
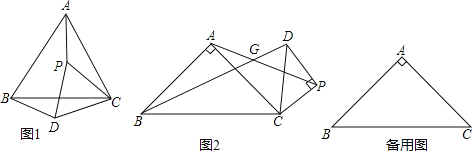
（1）观察猜想：如图1，当
时，线段绕点P顺时针旋转得到线段，则
的值是________，直线
与
相交所成的较小角的度数是________；
（2）类比探究：如图2，当
时，线段绕点P顺时针旋转得到线段．请直接写出与相交所成的较小角的度数，并说明
与
相似，求出的值；
（3）拓展延伸：当时，且点P到点C的距离为
，线段绕点P逆时针旋转得到线段，若点A，C，P在一条直线上时，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】民间素有“肖县石榴砀山梨，汴梁西瓜红到皮”的谚语，汴梁西瓜是开封的传统特产，驰名古今，畅销中外，某批发商先购买了300千克黑皮无籽西瓜和200千克花皮无籽西瓜，共花费520元，几天后又购买了400千克黑皮无籽西瓜和300千克花皮无籽西瓜，共花费720元（每次两种西瓜的批发价不变），
（1）求黑皮无籽西瓜和花皮无籽西瓜的批发价分别是每千克多少元；
（2）该批发商一段时间后为满足市场需求，还需购买两种西瓜共800千克，要求黑皮无籽西瓜的数量不少于花皮西瓜的3倍，请设计一种购买方案，使所需总费用最低．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了提高学生体育中考成绩，某学校打算购买A，B品牌实心球用于学生训练，若一次购买A品牌10个和B品牌5个，需花费350元；若一次购买A品牌4个和B品牌7个，需花费290元．
（1）求A品牌实心球和B品牌实心球的单价．
（2）现学校决定一次性购买A，B品牌实心球共50个，要求A品牌实心球数量不超过B品牌实心球数量的
倍，问如何安排购买方案，使学校购买的总费用最少？最少为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
和
中，
，
且
，点
在的内部，连接
，
，
和
，并且
．
（观察猜想）
（1）如图①，当
时，线段与
的数量关系为_____，线段
的数量关系为_______________；
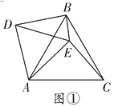
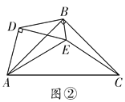
（探究证明）
（2）如图②，当
时，（1）中的结论是否依然成立？若成立，请给出证明，若不成立，请说明理由；
（拓展应用）
（3）在（2）的条件下，当点在线段
上时，若
，请直接写出
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小云在学习过程中遇到一个函数
．下面是小云对其探究的过程，请补充完整：
（1）当
时，对于函数
，即
，当时，
随
的增大而 ，且
；对于函数
，当时，
随的增大而 ，且
；结合上述分析，进一步探究发现，对于函数
，当时，随的增大而 ．
（2）当
时，对于函数，当时，与的几组对应值如下表：
| 0 |
| 1 |
| 2 |
| 3 |
|
| 0 |
|
|
| 1 |
|
|
|
综合上表，进一步探究发现，当时，随的增大而增大．在平面直角坐标系
中，画出当时的函数的图象．
（3）过点(0，m)（
）作平行于轴的直线
，结合（1）（2）的分析，解决问题：若直线与函数的图象有两个交点，则
的最大值是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某生产商存有1200千克
产品，生产成本为150元/千克，售价为400元千克.因市场变化，准备低价一次性处理掉部分存货，所得货款全部用来生产
产品，产品售价为200元/千克.经市场调研发现，产品存货的处理价格
（元/千克）与处理数量
（千克）满足一次函数关系（
），且得到表中数据.
|
|
200 | 350 |
400 | 300 |
（1）请求出处理价格（元千克）与处理数量（千克）之间的函数关系；
（2）若产品生产成本为100元千克，产品处理数量为多少千克时，生产产品数量最多，最多是多少？
（3）由于改进技术，产品的生产成本降低到了
元/千克，设全部产品全部售出，所得总利润为
（元），若
时，满足随的增大而减小，求的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
