
【题目】如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6CM.点P,Q同时由B,A两点出发,分别沿射线BC,AC方向以1cm/s的速度匀速运动. 
(1)几秒后△PCQ的面积是△ABC面积的一半?
(2)连结BQ,几秒后△BPQ是等腰三角形?
【答案】
(1)解:设运动x秒后,△PCQ的面积是△ABC面积的一半,
当0<x<6时,
S△ABC= ![]() ×ACBC=
×ACBC= ![]() ×6×8=24,
×6×8=24,
即: ![]() ×(8﹣x)×(6﹣x)=
×(8﹣x)×(6﹣x)= ![]() ×24,
×24,
x2﹣14x+24=0,
(x﹣2)(x﹣12)=0,
x1=12(舍去),x2=2;
当6<x<8时,
![]() ×(8﹣x)×(x﹣6)=
×(8﹣x)×(x﹣6)= ![]() ×24,
×24,
x2﹣14x+72=0,
b2﹣4ac=196﹣288=﹣92<0,
∴此方程无实数根,
当x>8时,
S△ABC= ![]() ×ACBC=
×ACBC= ![]() ×6×8=24,
×6×8=24,
即: ![]() ×(x﹣8)×(x﹣6)=
×(x﹣8)×(x﹣6)= ![]() ×24,
×24,
x2﹣14x+24=0,
(x﹣2)(x﹣12)=0,
x1=12,x2=2(舍去),
所以,当2秒或12秒时使得△PCQ的面积等于△ABC的面积的一半
(2)解:设t秒后△BPQ是等腰三角形,
①当BP=BQ时,t2=62+(8﹣t)2,
解得:t= ![]() ;
;
②当PQ=BQ时,(6﹣t)2+(8﹣t)2=62+(8﹣t)2,
解得:t=12;
③当BP=PQ时,t2=(6﹣t)2+(8﹣t)2,
解得:t=14±4 ![]() .
.

【解析】(1)设P、Q同时出发,x秒钟后,当0<x<6时,当6<x<8时,当x>8时,由此等量关系列出方程求出符合题意的值;(2)分别根据①当BP=BQ时,②当PQ=BQ时,③当BP=PQ时,利用勾股定理求出即可.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF. 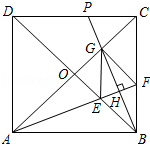
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
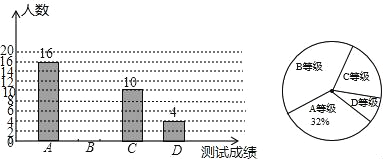
【题目】某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图;
(1)这次抽样调查的样本容量是 ,并补全条形图;
(2)D等级学生人数占被调查人数的百分比为 ,在扇形统计图中C等级所对应的圆心角为 °;
(3)该校九年级学生有1500人,请你估计其中A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 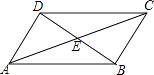
A.6
B.12
C.20
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点的位置如图所示,将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
利用网格点画图: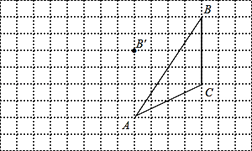
(1)画出△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com