
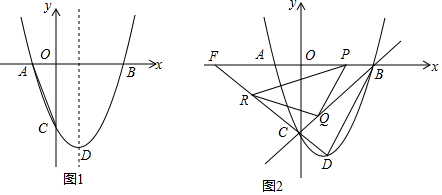
���� ��1����A��B��������꣬���ô���ϵ��������ö��κ����ı���ʽ��
��2����E��m��m2-2m-3��������E��EM��x�ᣬ��AD�ڵ�M���������ɵá�AOC��������Ӷ�����á�ADE����������ô���ϵ���������ֱ��AD�Ľ���ʽ�������m��ʾ��EM�ij����Ӷ�����m��ʾ����ADE��������Ӷ��ɵõ�����m�ķ��̣������m��ֵ��
��3����C��D��������ֱ��CD�Ľ���ʽ���Ӷ������F�����꣬�����OF=OC���ɵá�RFP=��RPQ=45�㣬�ɡ�PQR ���PFR ���Ƶõ�����PQR�ס�FRP ���PQR�ס�FPR��������������εĶ�Ӧ�߳ɱ����õ���P�����꣮
��� �⣺��1������A�͵�B��������������ߵĽ���ʽ��$\left\{\begin{array}{l}1-b+c=0\\ 9+3b+c=0\end{array}\right.$�����$\left\{\begin{array}{l}b=-2\\ c=-3\end{array}\right.$��
����κ����ı���ʽΪy=x2-2x-3��
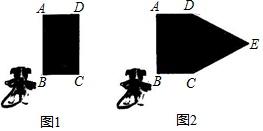
��2����E��m��m2-2m-3��������E��EM��x�ᣬ��AD�ڵ�M������ͼ1��
��y=x2-2x-3=�� x-1��2-4�ö���D��1��-4����C��0��-3����
��${S_{��AOC}}=\frac{1}{2}OA��OC=\frac{1}{2}��1��3=\frac{3}{2}$��
��S��ADE=2S��AOC=3��
��A��-1��0����D��1��-4����
��ֱ��ADΪ��y=-2x-2��
��E��m��m2-2m-3����
��M��$-\frac{1}{2}{m^2}+m+\frac{1}{2}$��m2-2m-3����
��EM=$m-��{-\frac{1}{2}{m^2}+m+\frac{1}{2}}��=\frac{1}{2}{m^2}-\frac{1}{2}$��
��S��ADE$\frac{1}{2}$��4��EM=2EM=m2-1=3��
���m=��2������m=-2��ȥ����
��E��2-3����
��3����C��0��-3����D��1��-4����
��ֱ��CD�Ľ���ʽΪ��y=-x-3��
��y=0ʱ��x=-3��
��F��0��-3����
��OF=OC=3��
���OFC=45�㣬����PFR=45�㣮
��PQ��BD��
���FPQ��90�㣬
���FPR��45�㣬
�൱��PQR ���PFR ����ʱ��
��PQR�ס�FRP����
��P�������ǣ�P1��$\frac{7}{3}$��0����P2��0��0����
���� ���⿼���˶��κ����ۺ��⣬����ʱ�ۺ������˴���ϵ��������κ�������ʽ�����κ���ͼ���ϵ��������������������������Լ����������ε����ʣ�ע�����������ѧ˼���Ӧ�ã��ѶȽϴ�


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
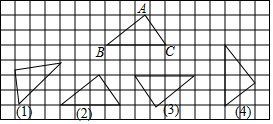 ͼ����ţ�1����2����3����4����Ӧ���ĸ������Σ����ǡ�ABC���ͼ�ν�����һ�α任֮��õ��ģ�������ͨ����ԳƵõ����ǣ�������
ͼ����ţ�1����2����3����4����Ӧ���ĸ������Σ����ǡ�ABC���ͼ�ν�����һ�α任֮��õ��ģ�������ͨ����ԳƵõ����ǣ�������| A�� | ��1�� | B�� | ��2�� | C�� | ��3�� | D�� | ��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���εĶԽ�����ƽ�� | |
| B�� | һ��Ա�ƽ�У�һ��Ա���ȵ��ı�����ƽ���ı��� | |
| C�� | �Խ����ഹֱ����ȵ��ı����������� | |
| D�� | �Խ�����ȵ��ı����Ǿ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{7}$ | B�� | $\frac{6}{7}$ | C�� | -$\frac{6}{7}$ | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
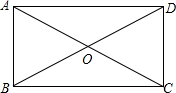 ��ͼ�����������У���ʹ?ABCD��Ϊ�����ǣ�������
��ͼ�����������У���ʹ?ABCD��Ϊ�����ǣ�������| A�� | AB=AD | B�� | ��ABO=60�� | C�� | AO=BO | D�� | AC��BD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��a��0������0��b��������a��b����|a+b-34|+|-a+b+18|=0������B����ƽ��24����λ�õ���C��
��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��a��0������0��b��������a��b����|a+b-34|+|-a+b+18|=0������B����ƽ��24����λ�õ���C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������y=ax2+bx+c��a��0�����䶥������Ϊ��1��n��������x���һ�������ڵ㣨3��0���ͣ�4��0��֮�䣬���н��ۣ�
��ͼ��������y=ax2+bx+c��a��0�����䶥������Ϊ��1��n��������x���һ�������ڵ㣨3��0���ͣ�4��0��֮�䣬���н��ۣ�| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���� | Ϥ�� | ŦԼ |
| ʱ��/ʱ | +2 | -13 |
| A�� | 6��16��1ʱ��6��15��10ʱ | B�� | 6��16��1ʱ��6��14��10ʱ | ||
| C�� | 6��15��21ʱ��6��15��10ʱ | D�� | 6��15��21ʱ��6��16��12ʱ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com