练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．对数轴上的点P进行如下操作：先把点P表示的数乘以$\frac{1}{3}$，再把所得数对应的点向右平移1个单位，得到点P的对应点P′，点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′，如图，若点A表示的数是-3，则点A′表示的数是0；若点B′表示的数是2，则点B表示的数是3．已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合，则点E表示的数是1.5．

    分析 根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B表示的数为a，根据题意列出方程求解即可得到点B表示的数，设点E表示的数为b，根据题意列出方程计算即可得解．

    解答 解：点A′：-3×$\frac{1}{3}$+1=-1+1=0，
    设点B表示的数为a，则$\frac{1}{3}$a+1=2，
    解得a=3，
    设点E表示的数为b，则$\frac{1}{3}$b+1=b，
    解得b=1.5．
    故答案为：0，3，1.5．

    点评 本题考查了数轴，数轴上点右边的总比左边的大的性质，读懂题目信息是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．已知|a|=3，|b|=4，且a＞0，b＜0，求a、b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，已知AB是⊙O的直径，点C，D在⊙O上，点E在⊙O外，∠EAC=∠B=60°．
    （1）求∠ADC的度数；
    （2）求证：AE是⊙O的切线；
    （3）当BC=4时，求劣弧$\widehat{AC}$的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．化简：
    （1）$\sqrt{\frac{32}{25{x}^{2}}}$（x＞0）；（2）$\sqrt{\frac{y}{12{x}^{2}}}$（x＞0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．比较各组数的大小：
    （1）-$\frac{8}{9}$与-$\frac{7}{8}$；
    （2）-$\frac{5}{9}$与-0.555；
    （3）-（+4$\frac{2}{9}$）与-|-4$\frac{1}{4}$|

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年湖北省枝江市九校七年级3月联考数学试卷（解析版） 题型：单选题

    如图，直线a，b相交于点O，若∠1等于40°，则∠2等于（ ）

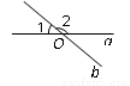
    A. 50° B. 60° C. 140° D. 160°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算下列各题
    （1）（3$\sqrt{2}$-$\sqrt{6}$）（$\sqrt{6}$+3$\sqrt{2}$）
    （2）（$\sqrt{12}$-$\sqrt{\frac{4}{3}}$-2（$\sqrt{\frac{1}{8}}$-$\frac{1}{\sqrt{2}}$-$\sqrt{18}$）+$\frac{1}{\sqrt{3}+2}$
    （3）（$\frac{1}{3}$）-1-（2015+$\sqrt{2}$）0+（-2）-2×$\sqrt{\frac{1}{16}}$+$\frac{1}{\sqrt{2}-1}$
    （4）（3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$）÷2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）-（-12）+（+18）-（+37）+（-41）
    （2）-12×（$\frac{1}{6}$+$\frac{1}{48}$）-49$\frac{3}{28}$÷（-5）2
    （3）-12×|1-$\frac{17}{15}}$|+$\frac{3}{4}$×[（-$\frac{2}{3}$）2-8]．
    （4）-32×1.22÷（-0.3）3+（-$\frac{1}{3}$）2×（-3）3÷（-1）25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．求满足下列条件的x的值．
    （1）x3=25；
    （2）8x3+27=0；
    （3）13（2x-1）3=104；
    （4）216x3+1=0．

    查看答案和解析>>

    同步练习册答案