
【题目】如图,抛物线y= ![]() (x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.
【答案】
(1)
解:顶点D的坐标为(3,﹣1).
令y=0,得 ![]() (x﹣3)2﹣1=0,
(x﹣3)2﹣1=0,
解得:x1=3+ ![]() ,x2=3﹣
,x2=3﹣ ![]() ,
,
∵点A在点B的左侧,
∴A(3﹣ ![]() ,0),B(3+
,0),B(3+ ![]() ,0)
,0)
(2)
方法一:
证明:如答图1,过顶点D作DG⊥y轴于点G,则G(0,﹣1),GD=3.

令x=0,得y= ![]() ,
,
∴C(0, ![]() ).
).
∴CG=OC+OG= ![]() +1=
+1= ![]() ,
,
∴tan∠DCG= ![]() .
.
设对称轴交x轴于点M,则OM=3,DM=1,AM=3﹣(3﹣ ![]() )=
)= ![]() .
.
由OE⊥CD,易知∠EOM=∠DCG.
∴tan∠EOM=tan∠DCG= ![]() =
= ![]() ,
,
解得EM=2,
∴DE=EM+DM=3.
在Rt△AEM中,AM= ![]() ,EM=2,由勾股定理得:AE=
,EM=2,由勾股定理得:AE= ![]() ;
;
在Rt△ADM中,AM= ![]() ,DM=1,由勾股定理得:AD=
,DM=1,由勾股定理得:AD= ![]() .
.
∵AE2+AD2=6+3=9=DE2,
∴△ADE为直角三角形,∠EAD=90°.
设AE交CD于点F,
∵∠AEO+∠EFH=90°,∠ADC+AFD=90°,∠EFH=∠AFD(对顶角相等),
∴∠AEO=∠ADC
方法二:
∵C(0, ![]() ),D(3,﹣1),
),D(3,﹣1),
∴KCD= ![]() ,
,
∵OE⊥CD,∴KCD×KOE=﹣1,
∴KOE= ![]() ,
,
∴lOE:y= ![]() x,把x=3代入,得y=2,
x,把x=3代入,得y=2,
∴E(3,2),
∵A(3﹣ ![]() ,0),D(3,﹣1),
,0),D(3,﹣1),
∴KEA= ![]() =
= ![]() ,
,
∵KAD= ![]() ,
,
∴KEA×KAD=﹣1,
∴EA⊥AD,∠EHD=∠EAD,
∵∠EFH=∠AFD,
∴∠AEO=∠ADC
(3)
方法一:
解:依题意画出图形,如答图2所示:

由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2﹣1,
要使切线长PQ最小,只需EP长最小,即EP2最小.
设点P坐标为(x,y),由勾股定理得:EP2=(x﹣3)2+(y﹣2)2.
∵y= ![]() (x﹣3)2﹣1,
(x﹣3)2﹣1,
∴(x﹣3)2=2y+2.
∴EP2=2y+2+(y﹣2)2=(y﹣1)2+5
当y=1时,EP2有最小值,最小值为5.
将y=1代入y= ![]() (x﹣3)2﹣1,得
(x﹣3)2﹣1,得 ![]() (x﹣3)2﹣1=1,
(x﹣3)2﹣1=1,
解得:x1=1,x2=5.
又∵点P在对称轴右侧的抛物线上,
∴x1=1舍去.
∴P(5,1).
∵△EQ2P为直角三角形,
∴过点Q2作x轴的平行线,再分别过点E,P向其作垂线,垂足分别为M点和N点.
由切割线定理得到Q2P=Q1P=2,EQ2=1
设点Q2的坐标为(m,n)
则在Rt△MQ2E和Rt△Q2NP中建立勾股方程,即(m﹣3)2+(n﹣2)2=1①,(5﹣m)2+(n﹣1)2=4②
①﹣②得n=2m﹣5③
将③代入到①得到
m1=3(舍,为Q1)
m2= ![]()
再将m= ![]() 代入③得n=
代入③得n= ![]() ,
,
∴Q2( ![]() ,
, ![]() )
)
此时点Q坐标为(3,1)或( ![]() ,
, ![]() )
)
方法二:由⊙E的半径为1,得PQ2=EP2﹣1,要使切线长PQ最小,只需EP长最小,即EP2最小,
设点P坐标为(x,y),EP2=(x﹣3)2+(y﹣2)2,
∵y= ![]() (x﹣3)2﹣1,∴(x﹣3)2=2y+2,
(x﹣3)2﹣1,∴(x﹣3)2=2y+2,
∴EP2=2y+2+(y﹣2)2=(y﹣1)2+5,
∴当y=1时,EP2有最小值,将y=1代入y= ![]() (x﹣3)2﹣1得:x1=1,x2=5,
(x﹣3)2﹣1得:x1=1,x2=5,
又∵点P在对称轴右侧的抛物线上,
∴x1=1舍去,∴P(5,1),
显然Q1(3,1),
∵Q1Q2被EP垂直平分,垂足为H,
∴KQ1Q2×KEP=﹣1,
∴KEP= ![]() =﹣
=﹣ ![]() ,KQ1Q2=2,
,KQ1Q2=2,
∵Q1(3,1),
∴lQ1Q2:y=2x﹣5,
∵lEP:y=﹣ ![]() x+
x+ ![]() ,
,
∴x= ![]() ,y=
,y= ![]() ,
,
∴H( ![]() ,
, ![]() ),
),
∵H为Q1Q2的中点,
∴Hx= ![]() ,
,
HY= ![]() ,
,
∴Q2(x)=2× ![]() ﹣3=
﹣3= ![]() ,
,
Q2(Y)=2× ![]() ﹣1=
﹣1= ![]() ,
,
∴Q2( ![]() ,
, ![]() ).
).

【解析】(1)根据二次函数性质,求出点A、B、D的坐标;(2)如何证明∠AEO=∠ADC?如答图1所示,我们观察到在△EFH与△ADF中:∠EHF=90°,有一对对顶角相等;因此只需证明∠EAD=90°即可,即△ADE为直角三角形,由此我们联想到勾股定理的逆定理.分别求出△ADE三边的长度,再利用勾股定理的逆定理证明它是直角三角形,由此问题解决;(3)依题意画出图形,如答图2所示.由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2﹣1,要使切线长PQ最小,只需EP长最小,即EP2最小.利用二次函数性质求出EP2最小时点P的坐标,并进而求出点Q的坐标.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
等级 | 成绩x/分 | 频数/(人数) | 频率 |
A | 9.0≤x≤10.0 | a | m |
B | 7.0≤x<9.0 | 23 | 0.46 |
C | 6.0≤x<7.0 | b | n |
D | 0.0≤x<6.0 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)在被调查的男生中,成绩为B等级的有多少人,占被调查男生人数的多少,m 等于 多少;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.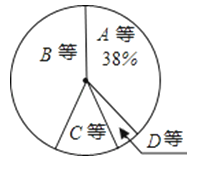
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按如表规律排列,表中数2在第二行第一列,与有序数对![]() 对应,数5与
对应,数5与![]() 对应,数14与
对应,数14与![]() 对应,根据这一规律,数2014对应的有序数对为__________.
对应,根据这一规律,数2014对应的有序数对为__________.
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ||
第一行 | 1 | 4 | 5 | 16 | 17 | … |
第二行 | 2 | 3 | 6 | 15 | … | |
第三行 | 9 | 8 | 7 | 14 | … | |
第四行 | 10 | 11 | 12 | 13 | … | |
第五行 | … | |||||
…… |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题: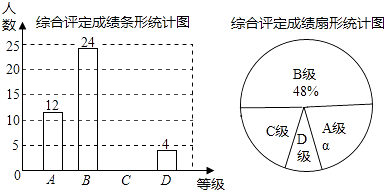
(1)在这次调查中,一共抽取了名学生,α=%;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为度;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=30°,点D在BC边上,点E在AC边上,AD=BD,DE=CE,若△ADE为等腰三角形,则∠C的度数为( )
A. 20° B. 20°或30° C. 30°或40° D. 20°或40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,且∠O=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH、…,添加的钢管长度都与OE相等,则最多能添加这样的钢管( )

A. 2根 B. 4根 C. 5根 D. 无数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰梯形ABCD中,AD∥BC,∠B=45°,P是BC边上一点,△PAD的面积为 ![]() ,设AB=x,AD=y
,设AB=x,AD=y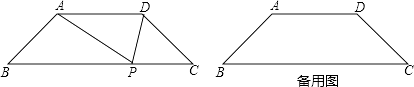
(1)求y与x的函数关系式;
(2)若∠APD=45°,当y=1时,求PBPC的值;
(3)若∠APD=90°,求y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)材料1:一般地,n个相同因数a相乘:![]() 记为
记为 ![]() 如
如![]() ,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,
,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,![]() =________;
=________;
(2)材料2:新规定一种运算法则:自然数1到n的连乘积用n!表示,例如:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…在这种规定下,请你解决下列问题:
①算5!=________;
②已知x为整数,求出满足该等式的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,则CE的长为( )
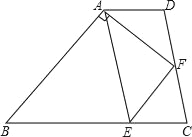
A. 2![]() B. 2
B. 2![]() -1 C. 2.5 D. 2.3
-1 C. 2.5 D. 2.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com