
如图,在平面直角坐标系xOy中,抛物线 的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?
解:(1)当m=2时,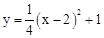 ,
,
把x=0代入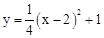 ,得:y=2,
,得:y=2,
∴点B的坐标为(0,2)。
(2)延长EA,交y轴于点F,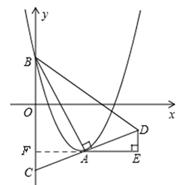
∵AD=AC,∠AFC=∠AED=90°,∠CAF=∠DAE,
∴△AFC≌△AED(AAS)。∴AF=AE。
∵点A(m,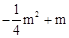 ),点B(0,m),
),点B(0,m),
∴AF=AE=|m|,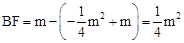 ,
,
∵∠ABF=90°﹣∠BAF=∠DAE,∠AFB=∠DEA=90°,
∴△ABF∽△DAE,∴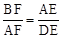 ,即:
,即: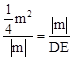 。∴DE=4。
。∴DE=4。
(3)①∵点A的坐标为(m,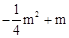 ),∴点D的坐标为(2m,
),∴点D的坐标为(2m,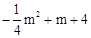 )。
)。
∴x=2m,y=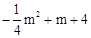 ,
,
∴y=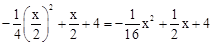 ,
,
∴所求函数的解析式为:y=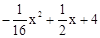 。
。
②作PQ⊥DE于点Q,则△DPQ≌△BAF,
(Ⅰ)当四边形ABDP为平行四边形时(如图1),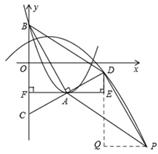
点P的横坐标为3m,
点P的纵坐标为: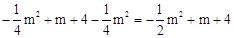 ,
,
把P(3m,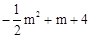 )代入y=
)代入y=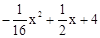 得:
得: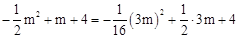 。
。
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=8。
(Ⅱ)当四边形ABDP为平行四边形时(如图2),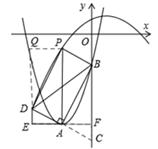
点P的横坐标为m,
点P的纵坐标为: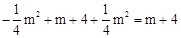 ,
,
把P(m,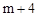 )代入
)代入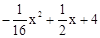 得:
得: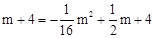 。
。
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=﹣8。
综上所述:m的值为8或﹣8。
解析


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.(假设年租金的增加额均为5000元的整数倍)该公司要为租出的商铺每间每年交各种费用2万元,未租出的商铺每间每年交各种费用1万元.
(1)当每间商铺的年租金定为12万元时,能租出多少间?年收益多少万元?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益最大,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,曲线 是函数
是函数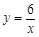 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数 的图象.点
的图象.点 (
( )在曲线
)在曲线 上,且
上,且 都是整数.
都是整数.
(1)求出所有的点 ;
;
(2)在 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数;
(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形
.是否存在点P,使四边形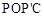 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,已知抛物线C经过原点,对称轴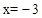 与抛物线相交于第三象限的点M,与x轴相交于点N,且
与抛物线相交于第三象限的点M,与x轴相交于点N,且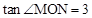 。
。
(1)求抛物线C的解析式;
(2)将抛物线C绕原点O旋转1800得到抛物线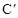 ,抛物线
,抛物线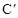 与x轴的另一交点为A,B为抛物线
与x轴的另一交点为A,B为抛物线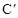 上横坐标为2的点。
上横坐标为2的点。
①若P为线段AB上一动点,PD⊥y轴于点D,求△APD面积的最大值;
②过线段OA上的两点E、F分别作x轴的垂线,交折线O-B-A于E1、F1,再分别以线段EE1、FF1为边作如图2所示的等边△AE1E2、等边△AF1F2,点E以每秒1个长度单位的速度从点O向点A运动,点F以每秒1个长度单位的速度从点A向点O运动,当△AE1E2有一边与△AF1F2的某一边在同一直线上时,求时间t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线 与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
(1)求点P运动的速度是多少?
(2)当t为多少秒时,矩形PEFQ为正方形?
(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0, ),点M是抛物线C2:
),点M是抛物线C2: (
( <0)的顶点.
<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;
(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | |
| 销售玩具获得利润w(元) | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com