练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．光线在不同介质中的传播速度不同，因此当光线从水中射向空气时，要发生折射．由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，当∠1=45°，∠2=122°时，∠3和∠4的度数分别是（　　）
    A．58°，122°B．45°，68°C．45°，58°D．45°，45°

    分析 先根据EG∥FH得出∠3的度数，再由AB∥CD得出∠ECD的度数，根据CE∥DF即可得出结论．

    解答 解：∵EG∥FH，∠1=45°，
    ∴∠3=∠1=45°．
    ∵AB∥CD，∠2=122°，
    ∴∠ECD=180°-122°=58°．
    ∵CE∥DF，
    ∴∠4=∠ECD=58°．
    故选C．

    点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．如图，直线l1∥l2，∠A=125°，∠B=105°，则∠1+∠2=（　　）°．
    A．230B．20C．50D．90

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，在梯形ABCD中，AD∥BC，AD=1，BC=4，AC=3，BD=4，则梯形ABCD的面积为6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．命题“如果两个实数的平方相等，那么这两个实数相等”，其逆命题是“如果这两个实数相等，那么这两个实数的平方相等”．逆命题是真 命题（填“真”或“假”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知线段a；请你按下列步骤画图：（用圆规、三角板、量角器等工具画图，不写画法，只保留画图痕迹）
    ①画线段AB=a；
    ②画线段AB的中点O；
    ③延长线段AB到点E，使BE=AB；
    ④画∠AOB的平分线OM；
    ⑤以O为交点画出表示东南西北的十字线（按照上北下南，左西右东的规定），画出表示北偏西30°的射线OC；
    ⑥过点B，画PQ∥OC，交直线OM于点G；
    ⑦写出图形中与∠AOC互余的角；
    ⑧写出图形中∠GBO和∠QBE之间的位置关系和数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．（-$\sqrt{7}$）2-$\sqrt{{6}^{2}}$+$\root{3}{-8}$=7-6-2（书写每项化简过程）=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

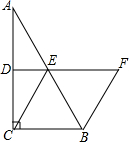    5．如图，在△ABC中，∠ACB=90°，D，E分别为AC，AB的中点，BF∥CE交DE的延长线于点F．
    （1）求证：四边形ECBF是平行四边形；
    （2）当∠A=30°时，求证：四边形ECBF是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

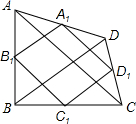    9．如图，四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm，点A1，B1，C1，D1是四边形ABCD各边上的中点，则四边形A1B1C1D1的周长为9cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，在每个小正方形的边长为1的网格中，A，E为格点，B，F为小正方形边的中点，C为AE，BF的延长线的交点．
    （Ⅰ）AE的长等于$\sqrt{5}$；
    （Ⅱ）若点P在线段AC上，点Q在线段BC上，且满足AP=PQ=QB，请在如图所示的网格中，用无刻度的直尺，画出线段PQ，并简要说明点P，Q的位置是如何找到的（不要求证明）AC与网格线相交，得到P，取格点M，连接AM，并延长与BC交于Q，连接PQ，则线段PQ即为所求．

    查看答案和解析>>

    同步练习册答案