
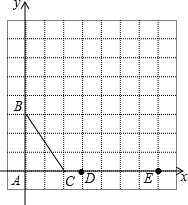
 如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6).
如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6). 分析 利用∠PDE=90°,$\frac{PD}{AB}$=$\frac{DE}{AC}$可判断△PDE∽△BAC,根据相似比计算出PD,从而得到一个符合条件的点P的坐标.
解答 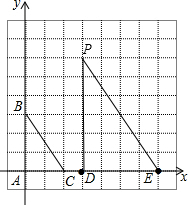 解:AB=3,AC=4,∠BAC=90°,DE=4,
解:AB=3,AC=4,∠BAC=90°,DE=4,
若∠PDE=90°,$\frac{PD}{AB}$=$\frac{DE}{AC}$时,△PDE∽△BAC,即$\frac{PD}{3}$=$\frac{4}{2}$,解得PD=6,
此时P点坐标为(3,6),
所以当点P坐标为(3,6)时,使△ABC与以E、P、D为顶点的三角形相似.
故答案为(3,6).
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了坐标与图形性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.
如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com