
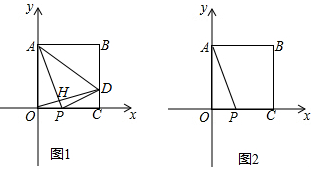
分析 (1)根据抛物线y=-(x-h)2+k经过A、B两点,即可得到抛物线的对称轴,把点B坐标(10,10)代入,即可得到抛物线函数关系式;
(2)先根据△AOP≌△OCD,得出OP=CD=t,进而得到CP=10-t,BD=10-t,再根据S△ADP=S正方形ABCO-S△AOP-S△ABD-S△CDP,可得当0≤t≤10时,S=$\frac{1}{2}$t2-5t+50,最后配方,得S的最小值;
(3)①根据点Q落在⊙A上时t的值,以及点P与点C重合,与点B重合时t的值,即可得到线段PQ与⊙A只有一个公共点时,t的取值范围,以及线段PQ与⊙A有两个公共点时,t的取值范围;②证明线段与圆由2个公共点需要证明两点:圆与线段所在直线相交(有2个公共点);线段的两端点都在圆外.
解答 解:(1)∵抛物线y=-(x-h)2+k经过A、B两点,
∴根据对称性可知h=5,
将B(10,10)代入y=-(x-5)2+k,可得10=-25+k,
解得k=35,
∴抛物线函数关系式为y=-(x-5)2+35;
(2)如图1,∵OD⊥AP,∠AOP=90°,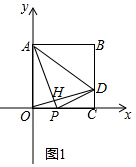
∴∠OAP+∠AOD=∠COD+∠AOD=90°,
∴∠OAP=∠COD,
又∵∠AOP=∠OCD=90°,AO=OC,
∴△AOP≌△OCD,
∴OP=CD=t,
∴CP=10-t,BD=10-t,
∵S△ADP=S正方形ABCO-S△AOP-S△ABD-S△CDP,
∴当0≤t≤10时,S=10×10-$\frac{1}{2}$×10t-$\frac{1}{2}$t(10-t)-$\frac{1}{2}$×10(10-t)=$\frac{1}{2}$t2-5t+50,
配方,得S=$\frac{1}{2}$(t-5)2+$\frac{75}{2}$,
∴当t=5时,Smin=$\frac{75}{2}$;
(3)①如图,当点Q在⊙A上时,连接AQ,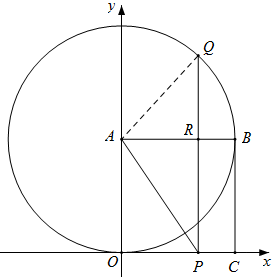
∵PQ=12+t,PR=BC=10,
∴RQ=2+t,
又∵AQ=AB=10,AR=OP=t,
∴Rt△ARQ中,t2+(t+2)2=102,
解得t1=6,t2=-8(舍去),
∴当t=6时,点Q落在⊙A上;
如图,当P在CB上时,CQ与⊙A相切,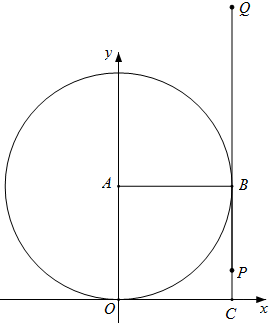
当点P与点C重合时,t=10;当点P与点B重合时,t=20;
∴当0≤t<6或10≤t≤20时,线段PQ与⊙A只有一个公共点;
当6≤t<10时,线段PQ与⊙A有两个公共点;
②如图,当6≤t<10时,AR=t<10,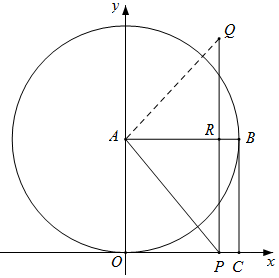
∴⊙A与直线PQ相交,
又∵AP2=AO2+OP2=100+t2,即AP>10,
∴点P在⊙A外,
又∵AQ2=AR2+RQ2=t2+(t+2)2,r2=100,
∴AQ2-r2=t2+(t+2)2-100=2(t+1)2-98,
∴当6≤t<10时,2(t+1)2-98≥0,
∴点Q在⊙A上或⊙A外,
综上所述,当6≤t<10时,线段PQ与⊙A总有两个公共点.
点评 本题属于二次函数综合题,主要考查了待定系数法的运用,二次函数的最值,直线与圆的位置关系以及勾股定理的综合应用,解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查一架“歼20”战机各零部件的产品质量 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查市场上酸奶的质量情况 | |
| D. | 调查我市市民对上届巴西奥运会吉祥物的知晓度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
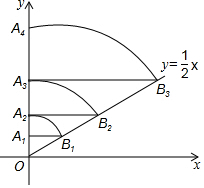 如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )| A. | ($\sqrt{5}$)2016 | B. | ($\sqrt{5}$)2017 | C. | 22016 | D. | 22017 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com