
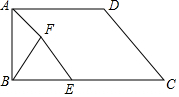
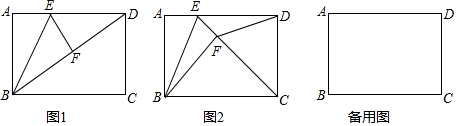
 ��ͼ��ʾ����֪����ABCD�У�AD��BC����ABC=90�㣬AD=7��BC=10��CD=6��E��BC����һ���㣬��BEΪһ����BC�Ϸ����ȱߡ�BEF������AF��
��ͼ��ʾ����֪����ABCD�У�AD��BC����ABC=90�㣬AD=7��BC=10��CD=6��E��BC����һ���㣬��BEΪһ����BC�Ϸ����ȱߡ�BEF������AF������ ��1�������CH�������ù��ɶ����ó�DH���ɵó�AB�����ɵó����ۣ�
��2�����ɵȱ������ε����ʵó�FM��BM��BG����������������ε����ʽ������̼��ɵó�������ϵʽ����x+y��10ȷ�����Ա����ķ�Χ��
��3����������������ߵ����ʼ��ȱ������ε����ʼ������BE��
��� �⣨1����ͼ1��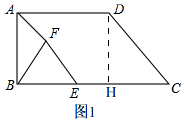 ����D��DH��BC��
����D��DH��BC��
���DHB=��DHC=90�㣬
��AD��BC��
���ABC=��BAD=90�㣬
���ı���ABHD�Ǿ��Σ�
��BH=AD=7��DH=AB��
��CH=BC-BH=10-7=3
����Rt��CDH��CH=3��CD=6��
��DH=3$\sqrt{3}$��
��AB=DH=3$\sqrt{3}$��
�ߡ�BEF�ǵȱ������Σ�
���EBF=60�㣬
���ABF=30�㣬
��BF��AF��
���AFB=90�㣬
��AF=$\frac{1}{2}$AB=$\frac{3\sqrt{3}}{2}$��
��BF=$\sqrt{3}$AF=$\frac{9}{2}$��
��2����ͼ2��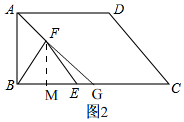 ����F��FM��BC��
����F��FM��BC��
�ߡ�BEF�ǵȱ������Σ�
��BM=EM=$\frac{1}{2}$BE=$\frac{1}{2}$x��FM=$\frac{\sqrt{3}}{2}$x��
��EG=y��
��GM=$\frac{1}{2}$x+y��GB=x+y
��FM��BC��AB��BC��
��FM��AB��
���GMF�ס�GBA��
��$\frac{GM}{GB}=\frac{FM}{AB}$����$\frac{\frac{1}{2}x+y}{x+y}=\frac{\frac{\sqrt{3}}{2}x}{3\sqrt{3}}$��
��y=$\frac{{x}^{2}-3x}{6-x}$��
��AF����BC�ڵ�G��
��x+y��10��
��x+$\frac{{x}^{2}-3x}{6-x}$��10��
��x��$\frac{60}{13}$����0��x��$\frac{60}{13}$��
����y=$\frac{{x}^{2}-3x}{6-x}$��0��x��$\frac{60}{13}$����
��3�� �ɣ�2��֪��BM=x��FM=$\frac{\sqrt{3}}{2}$x��
�ɣ�2��֪��BM=x��FM=$\frac{\sqrt{3}}{2}$x��
��BM��FM��
���F�����ܺ�AB��BCͬʱ���У�
����ͼ3������F��AB��ADͬʱ����ʱ����FP=FQ��FP��AB��FQ��AD��
�ɣ�2��֪��FP=BM=$\frac{1}{2}$BE��FM=$\frac{\sqrt{3}}{2}$BE��
��QM=AB=3$\sqrt{3}$��
��FQ=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$BE��
��$\frac{1}{2}$BE=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$BE��
��BE=9-3$\sqrt{3}$��
����ͼ4��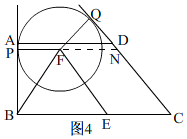 ����F��AB��CDͬʱ����ʱ��
����F��AB��CDͬʱ����ʱ��
��FP=FQ����FQC=90�㣬
��ͼ1�У���Rt��CHD�У�CD=6��CH=3��
���CDH=30�㣬
���C=60�㣬
�ߡ�BEF=60�㣬
��EF��CD���ӳ�PF��CD��N��
��FN��BC��
���ı���CDFE��ƽ���ı��Σ�
��FN=EC=10-BE����FDQ=60�㣬
��Rt��DQF��sin��FDQ=sin60��=$\frac{FQ}{FN}$��
��FQ=FP=$\frac{1}{2}$BE��
��$\frac{\sqrt{3}}{2}$=$\frac{\frac{1}{2}BE}{10-BE}$��
��BE=15-5$\sqrt{3}$��
������F����������ͬʱ����ʱ��BEΪ9-3$\sqrt{3}$��15-5$\sqrt{3}$��
���� ������Բ���ۺ��⣬��Ҫ�����˾��ε��ж����ȱ������ε����ʣ����������ε��ж������ʣ����ɶ�������30���ֱ�������ε����ʣ��Ȿ��Ĺؼ����ú�30���ֱ�������ε���������߶εij�����һ���е��Ѷȵĺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
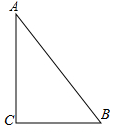 ��ͼ����Rt��ABC�У���C=90�㣬AB=8����A=30�㣬��BC=��������
��ͼ����Rt��ABC�У���C=90�㣬AB=8����A=30�㣬��BC=��������| A�� | 8 | B�� | 6 | C�� | 4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
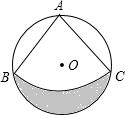 ��ͼ����Oֱ��Ϊ1�ף��ڡ�O����һ��Բ�Ľ���90�������ABC���ҵ�A��B��C�ڡ�O�ϣ����㻡AB�ij�����Ӱ�����
��ͼ����Oֱ��Ϊ1�ף��ڡ�O����һ��Բ�Ľ���90�������ABC���ҵ�A��B��C�ڡ�O�ϣ����㻡AB�ij�����Ӱ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
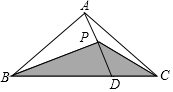 ��ͼ���ڡ�ABC�У���DΪBC����һ�㣬����AD��ȡAD���е�P������BP��CP������ABC�����Ϊ4cm2�����BPC�����Ϊ��������
��ͼ���ڡ�ABC�У���DΪBC����һ�㣬����AD��ȡAD���е�P������BP��CP������ABC�����Ϊ4cm2�����BPC�����Ϊ��������| A�� | 4cm2 | B�� | 3cm2 | C�� | 2cm2 | D�� | 1cm2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com