
分析 (1)根据两连续奇数乘积的倒数等于各自倒数差的一半可得;
(2)利用以上规律化简原分式方程得$\frac{1}{x}$-$\frac{1}{x+9}$=$\frac{3}{x+9}$,再根据解分式方程的步骤解答可得.
解答 解:(1)由题意知,在和式$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…中第6项为$\frac{1}{11×13}$,第n项为$\frac{1}{(2n-1)(2n+1)}$,
故答案为:$\frac{1}{11×13}$,$\frac{1}{(2n-1)(2n+1)}$;
(2)原方程可整理为:$\frac{1}{2}$($\frac{1}{x}$-$\frac{1}{x+3}$)+$\frac{1}{2}$($\frac{1}{x+3}$-$\frac{1}{x+6}$)+$\frac{1}{2}$($\frac{1}{x+6}$-$\frac{1}{x+9}$)=$\frac{3}{2x+18}$,
$\frac{1}{2}$($\frac{1}{x}$-$\frac{1}{x+3}$+$\frac{1}{x+3}$-$\frac{1}{x+6}$+$\frac{1}{x+6}$-$\frac{1}{x+9}$)=$\frac{3}{2x+18}$,
$\frac{1}{2}$($\frac{1}{x}$-$\frac{1}{x+9}$)=$\frac{3}{2(x+9)}$,
$\frac{1}{x}$-$\frac{1}{x+9}$=$\frac{3}{x+9}$,
两边都乘以x(x+9),得:x+9-x=3x,
解得:x=3,
经检验:x=3是原分式方程的解,
∴原分式方程的解为x=3.
点评 本题主要考查数字的变化规律和解分式方程,根据题意得出规律:两连续奇数乘积的倒数等于各自倒数差的一半,并利用此规律将原分式方程化简是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )
如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18′27″,则∠2度数是( )| A. | 25°18′27″ | B. | 64°41′33″ | C. | 74°4133″ | D. | 64°41′43″ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
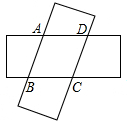 如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.
如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
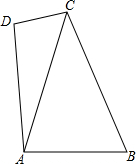 如图,在△ABC中,AC=BC=4,将线段AB绕点A逆时针旋转90°,连接CD,则线段CD的最小值是( )
如图,在△ABC中,AC=BC=4,将线段AB绕点A逆时针旋转90°,连接CD,则线段CD的最小值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$-2 | D. | 4$\sqrt{2}$-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com