
分析 (1)因为直线过(0,0),因此此函数是正比例函数,设解析式:y=kx(k≠0),把B$(3\sqrt{3},3)$代入可解出k的值,进而可得答案;
(2)根据A、B两点坐标可得AB的长,再由三角形是等边三角形可得C点坐标.
解答 解:(1)设直线AB的解析式:y=kx(k≠0),
把B$(3\sqrt{3},3)$代入得:$3=3\sqrt{3}k$,
解得$k=\frac{{\sqrt{3}}}{3}$.
∴AB直线的解析式为$y=\frac{{\sqrt{3}}}{3}x$.
(2)∵A(0,0),B($3\sqrt{3}$,3),
∴$AB=\sqrt{{{(3\sqrt{3})}^2}+{3^2}}=\sqrt{27+9}=6$,
∵△ABC是等边三角形,
∴$C(3\sqrt{3},-3)$和C(0,6).
点评 此题主要考查了待定系数法求一次函数解析式,以及等边三角形的判定,关键是掌握凡是经过原点的直线都是正比例函数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
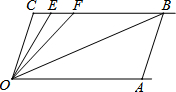 如图,已知直线BC∥OA,∠C=∠OAB=108°,E、F在线段BC上,且满足∠FOB=∠AOB,OE平分∠COF.
如图,已知直线BC∥OA,∠C=∠OAB=108°,E、F在线段BC上,且满足∠FOB=∠AOB,OE平分∠COF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com