
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
| 每月做家务总时间(分) | 洗碗次数 | 扫地的次数 | |
| 七年级 | 130 | 4 | 5 |
| 八年级 | 90 | 3 | 3 |
| 九年级 | 40 | a | b |
查看答案和解析>>
科目:初中数学 来源: 题型:
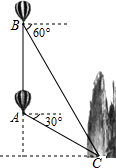 热气球探测器显示,热气球在点A处看到某小山底部点C的俯角为30°,后垂直上升一定高度至点B,看到点C的俯角为60°,热气球与小山的水平距离为1800米,如图,求热气球垂直上升的高度AB(结果精确到1米,参考数据
热气球探测器显示,热气球在点A处看到某小山底部点C的俯角为30°,后垂直上升一定高度至点B,看到点C的俯角为60°,热气球与小山的水平距离为1800米,如图,求热气球垂直上升的高度AB(结果精确到1米,参考数据| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
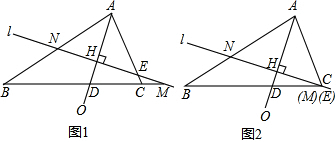
 如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF.
如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com