
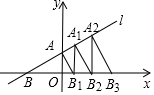
 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$. 分析 先根据直线的位置得到∠ABO=30°,BA=2,进而得出BB1=$\frac{4}{3}\sqrt{3}$,BB2=$\frac{16}{9}\sqrt{3}$,BB3=$\frac{64}{27}\sqrt{3}$,据此可得BBn=$(\frac{4}{3})^{n}\sqrt{3}$,根据BO=$\sqrt{3}$,可得OBn=$(\frac{4}{3})^{n}\sqrt{3}$-$\sqrt{3}$,进而得到点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}$-$\sqrt{3}$.
解答 解:由直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,可得A(0,1),B(-$\sqrt{3}$,0),
∴tan∠ABO=$\frac{\sqrt{3}}{3}$,即∠ABO=30°,
∴BA=2AO=2,
又∵AB1⊥AB交x轴于点B1,AO=1,
∴AB1=$\frac{2}{3}\sqrt{3}$,
∴Rt△BAB1中,BB1=$\frac{4}{3}\sqrt{3}$;
由题可得BA1=$\frac{8}{3}$,
∴A1B2=$\frac{8}{9}\sqrt{3}$,
∴Rt△BA1B2中,BB2=$\frac{16}{9}\sqrt{3}$;
由题可得BA2=$\frac{32}{9}$,
∴A2B3=$\frac{32}{27}\sqrt{3}$,
∴Rt△BA2B3中,BB3=$\frac{64}{27}\sqrt{3}$,
…
以此类推,BBn=$(\frac{4}{3})^{n}\sqrt{3}$,
又∵BO=$\sqrt{3}$,
∴OBn=$(\frac{4}{3})^{n}\sqrt{3}$-$\sqrt{3}$,
∴点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}$-$\sqrt{3}$,
故答案为:$(\frac{4}{3})^{n}\sqrt{3}$-$\sqrt{3}$.
点评 本题主要考查了一次函数图象上点的坐标特征以及点的坐标变化规律问题,解题的关键是依据含30°角的直角三角形的性质得出BBn=$(\frac{4}{3})^{n}\sqrt{3}$.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
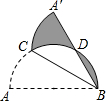 如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π.
如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
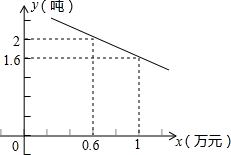 伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示.
伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com