
【题目】体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题: 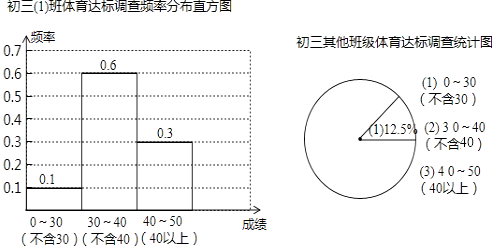
(1)初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?
(2)若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)
(3)如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求?
【答案】
(1)解:根据条形统计图得:初三(1)班学生体育达标率为0.6+0.3=0.9=90%;
根据扇形统计图得:本年级其余各班学生体育达标率为1﹣12.5%=87.5%;
答:初三(1)班学生体育达标率和本年级其余各班学生体育达标率分别是:90%、87.5%;
(2)解:其余各班的人数为530﹣50=480(人),
30﹣40分人数所占的角度为 ![]() ×360°=90°,
×360°=90°,
0﹣30分人数所占的角度为360×12.5%=45°,
30﹣40分人数所占的角度为360﹣90°﹣45°=225°,
补全扇形统计图,如图所示:

(3)解:由(1)知初三(1)班学生体育达标率为90%,由扇形统计图得到其余各班体育达标率为87.5%<90%,
则该年级全体学生的体育达标率不符合要求.
答:该年级全体学生的体育达标率不符合要求
【解析】(1)由频率分布直方图求出30分以上的频率,即为初三(1)班的达标率;由扇形统计图中30分以下的频率求出30分以上的频率,即为其余班的达标率;(2)根据30﹣40分的人数除以其余各班的人数求出所占的百分比,乘以360度,求出30﹣40分所占的角度,补全扇形统计图即可;(3)根据其余各班体育达标率小于90%,得到在本次调查中,该年级全体学生的体育达标率不符合要求.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量 | 年用水量 (立方米) | 水价 (元/立方米) |
第一阶梯 | 0~180(含) | 5.00 |
第二阶梯 | 181~260(含) | 7.00 |
第三阶梯 | 260以上 | 9.00 |
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2, ![]() ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1, ![]() ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.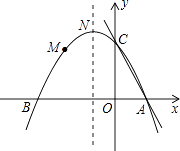
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60,得到△BAE,连接ED,若BC=5,BD=4,则有以下四个结论:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC。其中正确结论的序号是( )
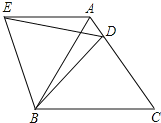
A. ②③④ B. ①③④ C. ①②④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A’B’C’,若它移动的距离AA’等于1cm,则两个三角形重叠部分的面积为____________cm2.
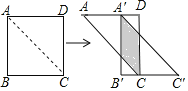
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,点C为圆上一点,将劣弧 ![]() 沿弦AC翻折交AB于点D,连结CD.
沿弦AC翻折交AB于点D,连结CD. 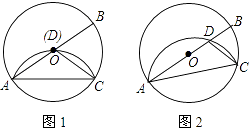
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,过点A、C、D作抛物线y=ax2+bx+c(a≠0),与x轴的另一交点为E,连结CE,点A、B、D的坐标分别为(﹣2,0)、(3,0)、(0,4).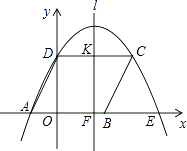
(1)求抛物线的解析式;
(2)已知抛物线的对称轴l交x轴于点F,交线段CD于点K,点M、N分别是直线l和x轴上的动点,连结MN,当线段MN恰好被BC垂直平分时,求点N的坐标;
(3)在满足(2)的条件下,过点M作一条直线,使之将四边形AECD的面积分为3:4的两部分,求出该直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,某市正在修建贯穿全城南北、东西的地铁1,2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元,且1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线、2号线每千米的平均造价分别是多少亿元;
(2)除1,2号线外,该市规划到2019年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com