
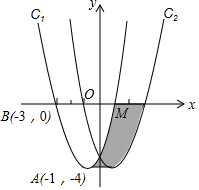
 如图,在平面直角坐标xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0).
如图,在平面直角坐标xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0).分析 (1)设抛物线C1的解析式为y=a(x+1)2-4,将B点代入解析式,求a,再由平移的规律得出C2的解析式,从而得出a,b,c的值;
(2)令y=5,得出x的值,根据图象得出ax2+bx+c>5的解集.
(3)阴影部分可以转换成求平行四边形的面积,即函数图象平移的距离乘以A点纵坐标的绝对值.
解答 解:(1)设抛物线C1的解析式为y=a(x+1)2-4,
将点B(-3,0)代入得a=1,
∴抛物线的解析式为y=(x+1)2-4,
∵将抛物线C1向右平移2个单位得抛物线C2,
∴抛物线C2的解析式为y=(x-1)2-4,
∴a,b,c的值分别为1,-2,-3;
(2)令y=(x-1)2-4中y=5,得x=4或-2.
∴x<-2或x>4时,ax2+bx+c>5,
即ax2+bx+c>5的解集为x<-2或x>4;
(3)阴影部分可以转换成求平行四边形的面积,S=2×|yA|=2×4=8,
故答案为x<-2或x>4,8.
点评 本题是二次函数的综合题,涉及知识点有抛物线的对称轴的求法,平移,面积求法等知识点.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
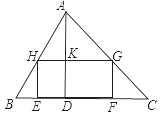 有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.
有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com