
【题目】在一次“构造勾股数”的探究性学习中,老师给出了下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() 、
、![]() 为正整数,且
为正整数,且![]() .
.
(![]() )观察表格,当
)观察表格,当![]() ,
, ![]() 时,此时对应的
时,此时对应的![]() 、
、![]() 、
、![]() 的值能否为直角三角形三边的长?说明你的理由.
的值能否为直角三角形三边的长?说明你的理由.
(![]() )探究
)探究![]() ,
, ![]() ,
, ![]() 与
与![]() 、
、![]() 之间的关系并用含
之间的关系并用含![]() 、
、![]() 的代数式表示:
的代数式表示: ![]() __________,
__________, ![]() __________,
__________, ![]() __________.
__________.
(![]() )以
)以![]() ,
, ![]() ,
, ![]() 为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
【答案】(1)是,理由见解析;(2)![]() ,
, ![]() ,
, ![]() ;(3)是直角三角形,理由见解析
;(3)是直角三角形,理由见解析
【解析】试题分析:(1)计算出a、b、c的值,根据勾股定理的逆定理判断即可;
(2)根据给出的数据总结即可;
(3)分别计算出a2、b2、c2,根据勾股定理的逆定理进行判断.
试题解析:
解:(1)当m=2,n=1时,a=5、b=4、c=3,
∵32+42=52,
∴a、b、c的值能为直角三角形三边的长;
(2)观察得,a=m2+n2,b=2mn,c=m2-n2;
(3)以a,b,c为边长的三角形一定为直角三角形,
∵a2=(m2+n2)2=m4+2m2n2+n4,
b2+c2=m4-2m2n2+n4+4m2n2= m4+2m2n2+n4,
∴a2=b2+c2,
∴a,b,c为边长的三角形一定为直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将7张如图1所示的长为a,宽为b(a>b)的小长方形纸片按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,求a,b满足的条件.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=﹣![]() x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
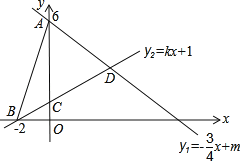
(1)m= ,k= ;
(2)求两直线交点D的坐标;
(3)根据图象直接写出y1<y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD平分∠ABC. 请补全图形后,依条件完成解答.
(1)在直线BC下方画∠CBE,使∠CBE与∠ABC互补;
(2)在射线BE上任取一点F,过点F画直线FG∥BD交BC于点G;
(3)判断∠BFG与∠BGF的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按![]() 不喜欢
不喜欢![]() 、
、![]() 一般
一般![]() 、
、![]() 不比较喜欢
不比较喜欢![]() 、
、![]() 非常喜欢
非常喜欢![]() 四个等级对该手机进行评价,图
四个等级对该手机进行评价,图![]() 和图
和图![]() 是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
![]() 本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
![]() 图
图![]() 中,a等于多少?D等级所占的圆心角为多少度?
中,a等于多少?D等级所占的圆心角为多少度?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com