
【题目】平面直角坐标系中,抛物线y=ax2+bx+2过点A(﹣3,0)、B (1,0),与y轴交于点C,抛物线的顶点为D,点G在抛物线上且其纵坐标为2.
(1)a= , b= , D( , ).
(2)P是线段AB上一动点(点P不与A、B重合),点P作x轴的垂线交抛物线于点E.
①若PE=PB,试求E点坐标;
②在①的条件下,PE、DG交于点M,在线段PE上是否存一点N,使得△DMN与△DCO相似?若存在,试求出相应点的坐标;
③在①的条件下,点F是坐标轴上一点,且点F到EC、ED的距离相等,试直接写出EF的长度.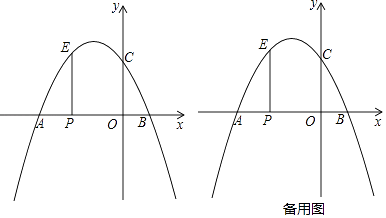
【答案】
(1)﹣ ![]() ;﹣
;﹣ ![]() ;﹣1;
;﹣1;![]()
(2)
①设P(x,0),则E(x,﹣ ![]() x2﹣
x2﹣ ![]() x+2),则PB=1﹣x,PE=﹣
x+2),则PB=1﹣x,PE=﹣ ![]() x2﹣
x2﹣ ![]() x+2.
x+2.
∵PE=PB,
∴﹣ ![]() x2﹣
x2﹣ ![]() x+2=1﹣x.
x+2=1﹣x.
∴x1=1(舍去),x2=﹣ ![]() .
.
当x=﹣ ![]() ,函数值y=
,函数值y= ![]() .
.
∴E(﹣ ![]() ,
, ![]() ).
).
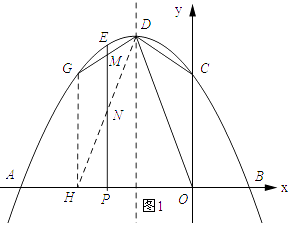
②存在点N(﹣ ![]() ,
, ![]() ),理由如下:过点G作GH⊥x轴,垂足为H,连结DH.
),理由如下:过点G作GH⊥x轴,垂足为H,连结DH.
把y=2代入抛物线的解析式得:2=﹣ ![]() x2﹣
x2﹣ ![]() x+2,解得x=0或x=﹣2.
x+2,解得x=0或x=﹣2.
∴G(﹣2,2).
抛物线的对称轴为x=﹣1,
∵GH⊥x轴,
∴H(﹣2,0).
∴△DOC与△DHG关于直线x=﹣1对称.
∴要使DMN与△DCO相似,只需△DMN与△DGH相似.
∵MN∥GH,
∴△DMN∽△DGH.
设直线DH的解析式为y=kx+b,将点H和点D的坐标代入得: 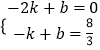 ,
,
解得:k= ![]() ,b=
,b= ![]() .
.
∴直线DH的解析式为y= ![]() x+
x+ ![]() .
.
将x=﹣ ![]() 代入得:y=
代入得:y= ![]() .
.
∴N(﹣ ![]() ,
, ![]() ).
).
③如图2所示:过点E作EF⊥y轴,交抛物线的对称轴与点G,则G(﹣1, ![]() )过点E作EF′⊥x垂足为F′.
)过点E作EF′⊥x垂足为F′.
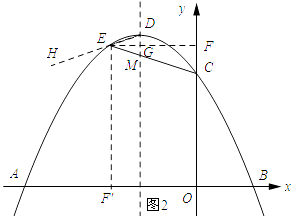
设直线EC的解析式为y=mx+n将点E和点C的坐标代入得: 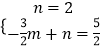 ,
,
解得:m=﹣ ![]() ,n=2.
,n=2.
∴直线EC的解析式为y= ![]() x+2.
x+2.
当x=﹣1时,y= ![]() .
.
∴DG=GM.
∴点M与点D关于EF对称.
∴EF是∠DEC的角平分线.
∴点F到点F到EC、ED的距离相等.
∴EF= ![]() .
.
∵EF′⊥x垂足为F′.
∴∠FEF′=90°,
∴∠DEF+∠HEF′=90°,∠FEC+∠CEF′=90°.
又∵∠DEF=∠FEC,
∴∠HEF′=∠CEF′.
∴EF′是∠HEC的平分线,
∴点F′到DE和EC的距离相等.
∴EF′= ![]() .
.
综上所述,EF的长为 ![]() 或
或 ![]() .
.
【解析】解:(1)把x=0代入抛物线的解析式得:y=2,
∴C(0,2).
设抛物线的解析式为y=a(x+3)(x﹣1),将点C的坐标代入得﹣3a=2,解得:a=﹣ ![]() .
.
∴抛物线的解析式为y=﹣ ![]() (x+3)(x﹣1)=﹣
(x+3)(x﹣1)=﹣ ![]() x2﹣
x2﹣ ![]() x+2.
x+2.
∴b=﹣ ![]() .
.
∴x=﹣ ![]() =﹣1.
=﹣1.
当x=﹣1时,y= ![]() .
.
∴D(﹣1, ![]() ).
).
所以答案是:﹣ ![]() ;﹣
;﹣ ![]() ;﹣1,
;﹣1, ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为 , 若A为随机事件,则m的取值为;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AC的垂直平分线上.
(1)若AB=AD,∠BAD=26°,求∠B和∠C的度数;
(2)若AB=AD=DC,AC=BC,求∠C的度数;
(3)若AC=6,△ABD的周长为13cm,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
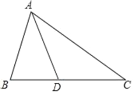
【题目】将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数,如数5对应的坐标为(-1,1),试探求2015对应的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
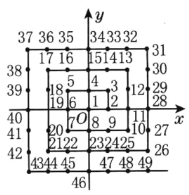
【题目】如图所示,一块广告牌AB顶端固定在一堵墙AD的A点处,与地面夹角∠ABD=45°,由于施工底部断裂掉一段以后,底部落在距离B点8米处的C点,此时与地面夹角∠ACD=75°.求断裂前、后的广告牌AB、AC的长度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )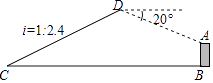
A.29.1米
B.31.9米
C.45.9米
D.95.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,平移三角形ABC,使点A平移到点![]() ,画出平移后的三角形
,画出平移后的三角形![]() ;
;
(2)在(1)的条件下,指出点A,B,C 的对应点,并指出AB,BC,AC的对应线段和∠A,∠B, ∠C的对应角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示. 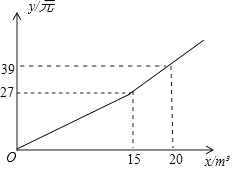
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com