
【题目】公园门票价格规定如下表:
![]()
某校七年级(1)、(2)两个班104人去游园,其中七(1)班不足50人,(2)班超过50人,但不足100人。经估算,如果两个班都以班为单位购票,则一共应付1240元。问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七(1)班单独组织去游园,作为组织者的你将如何购票才最省钱?
【答案】(1)七(1)班有48人,七(2)班有56人(2)团体购票可省304元(3)48人买51人的票可以更省钱
【解析】
(1)设七(1)班有x人,则七年级(2)班有(104-x)人,根据两个班都以班为单位购票,一共应付1240元列出方程,解方程即可;(2)根据100张以上每张9元求出两班联合起来,作为一个团体购票的费用,再比较即可得到结果;(3)分别计算出买48张票和51张票各自所需的费用,再比较即可得到结果.
(1)设七(1)班有![]() 人,根据题意得:
人,根据题意得:
![]()
![]()
![]() (人)
(人)
(2)![]() (元)
(元)
(3)因为七(1)班有48人,要想享受优惠,只需多买3张即可
![]() (元)
(元) ![]() (元)
(元)
答:七(1)班有48人,七(2)班有56人。团体购票可省304元。48人买51人的票可以更省钱。


科目:初中数学 来源: 题型:
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:

根据统计图提供的信息,解答下列问题:
(1)m= ,n= ;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)请根据以上信息补全条形统计图;
(4)根据抽样调查的结果,请你估计该校1000名学生中有多少学生最喜欢科普类图书.
【答案】 (1)m=50, n=30;(2)72度 (3)补图见解析(4)300
【解析】试题分析:(1)根据其他的人数和所占的百分比即可求得m的值,从而可以求得n的值;
(2)根据扇形统计图中的数据可以求得“艺术”所对应的扇形的圆心角度数;
(3)根据题意可以求得喜爱文学的人数,从而可以将条形统计图补充完整;
(4)根据统计图中的数据可以估计该校600名学生中有多少学生最喜欢科普类图书.
试题解析:
解:(1)m=5÷10%=50,n%=15÷50=30%,
故答案为:50,30;
(2)由题意可得,
“艺术”所对应的扇形的圆心角度数是:360°×![]() =72°,
=72°,
故答案为:72;
(3)文学有:50-10-15-5=20,
补全的条形统计图如图所示;

(4)由题意可得,
600×![]() =180,
=180,
即该校600名学生中有180名学生最喜欢科普类图书.
点睛:本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
【题型】解答题
【结束】
23
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.5元,花35元购买粽子的个数与花20元购买咸鸭蛋的个数相同.粽子与咸鸭蛋的价格各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚在课外书中看到这样一道有理数的混合运算题:
计算:![]()
她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,他顺利地解答了这道题。
(1)前后两部分之间存在着什么关系?
(2)先计算哪步分比较简便?并请计算比较简便的那部分。
(3)利用(1)中的关系,直接写出另一部分的结果。
(4)根据以上分析,求出原式的结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步了解某校七年级(2)班同学们的身体素质,体育老师对七年级(2)班的50名学生进行了一分钟跳绳次数测试,以测试成绩为样本,绘制出部分频数分布表和部分频数分布直方图,请结合两种图表完成下列问题:
(1)表中的a=
(2)把频数分布直方图补充完整
(3)若七年级学生每分钟跳绳的次数不小于120为合格,那么,这个七年级(2)班学生跳绳的合格率为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某文具商场中,每个画板定价为20元,每盒水彩笔定价为5元.为促进销售,商场制定两种优惠方案:一种是买一个画板赠送一盒水彩笔;另一种是按总价九折付款。王老师准备为学校美术小组购买画板4个,水彩笔若干盒(不少于4盒)。
(1)分别求出每种方案下王老师应支付多少元?(用代数式表示)
(2)如果购买24盒水彩笔,哪种方案更省钱?若买50盒水彩笔呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A. 商贩A的单价大于商贩B的单价
B. 商贩A的单价等于商贩B的单价
C. 商版A的单价小于商贩B的单价
D. 赔钱与商贩A、商贩B的单价无关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中信息解答下列问题: 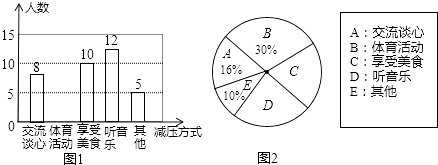
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”来减压方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ![]() ,求AQ的长.
,求AQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com