
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¶ž“ĪŗÆŹży£½x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć£¬AµćŌŚŌµćµÄ×ó²ą£¬BµćµÄ×ų±źĪŖ£Ø3£¬0£©£¬ÓėyÖį½»ÓŚC£Ø0£¬©3£©µć£¬µćPŹĒÖ±ĻßBCĻĀ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£®
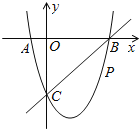
£Ø1£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½£®
£Ø2£©Į¬½ÓPO”¢PC£¬²¢°Ń”÷POCŃŲCO·ÕŪ£¬µĆµ½ĖıߊĪPOP”äC£¬ÄĒĆ“ŹĒ·ń“ęŌŚµćP£¬Ź¹ĖıߊĪPOP”äCĪŖĮāŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±µćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø3£©µ±µćPŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬ĖıߊĪABPCµÄĆ껿×ī“ó£æĒó³ö“ĖŹ±PµćµÄ×ų±źŗĶĖıߊĪABPCµÄ×ī“óĆ껿£®
”¾“š°ø”æ£Ø1£©y£½x2©2x©3£»£Ø2£©£Ø![]() £¬
£¬![]() £©£»£Ø3£©PµćµÄ×ų±źĪŖ
£©£»£Ø3£©PµćµÄ×ų±źĪŖ![]() £¬ĖıߊĪABPCµÄĆ껿µÄ×ī“óÖµĪŖ
£¬ĖıߊĪABPCµÄĆ껿µÄ×ī“óÖµĪŖ![]() £®
£®
”¾½āĪö”æ
£Ø1£©½«B”¢CĮ½µćµÄ×ų±ź“śČė½āĪöŹ½ÖŠ£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒó½ā¼“æÉ£»
£Ø2£©ŅŃÖŖŅŖŹ¹ĖıߊĪPOP”äCŹĒĮāŠĪ£¬ŌņPµćŅ»¶ØŌŚOCµÄ“¹Ö±Ę½·ÖĻßÉĻ£¬¾ĶæÉøł¾ŻCµćµÄ×ų±źÖŖµĄOCµÄ³¤¶Č£¬“Ó¶ųµĆµ½PµćµÄׯ×ų±ź£¬ŅŃÖŖPµćµÄׯ×ų±ź¾Ķ½«Ęä“śČė½āĪöŹ½ÖŠ¼“æÉĒóµĆPµć×ų±ź.
£Ø3£©¹żµćP×÷yÖįµÄĘ½ŠŠĻßÓėBC½»ÓŚµćQ£¬ÓėOB½»ÓŚµćF£¬ÉčPµć×ų±źĪŖ![]() £¬æÉĒó³öBCµÄ½āĪöŹ½“Ó¶ų±ķŹ¾³öQµćµÄ½āĪöŹ½£¬øł¾Ż
£¬æÉĒó³öBCµÄ½āĪöŹ½“Ó¶ų±ķŹ¾³öQµćµÄ½āĪöŹ½£¬øł¾Ż![]() æÉÓĆŗ¬ÓŠxµÄŹ½×Ó±ķŹ¾³öĖıߊĪABPCµÄĆ껿£¬×īŗóøł¾ŻŹ½×Ó·ÖĪö×ī“óÖµ¼“ĪŖĖıߊĪABCPĆ껿µÄ×ī“óÖµ£¬“ĖŹ±Ēó³öµÄx¼“ĪŖPµćµÄŗį×ų±ź£¬ŌŁ“śČė½āĪöŹ½¼“æÉĒó³öPµćµÄ×ų±ź¼“æÉ.
æÉÓĆŗ¬ÓŠxµÄŹ½×Ó±ķŹ¾³öĖıߊĪABPCµÄĆ껿£¬×īŗóøł¾ŻŹ½×Ó·ÖĪö×ī“óÖµ¼“ĪŖĖıߊĪABCPĆ껿µÄ×ī“óÖµ£¬“ĖŹ±Ēó³öµÄx¼“ĪŖPµćµÄŗį×ų±ź£¬ŌŁ“śČė½āĪöŹ½¼“æÉĒó³öPµćµÄ×ų±ź¼“æÉ.
½ā£ŗ£Ø1£©½«B”¢CĮ½µćµÄ×ų±ź“śČėµĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ![]() £»
£»
ĖłŅŌ¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½ĪŖ£ŗ![]() .
.
£Ø2£©“ęŌŚµćP£¬Ź¹ĖıߊĪPOP”äCĪŖĮāŠĪ£»
ÉčPµć×ų±źĪŖ![]() £¬PP”ä½»COÓŚE
£¬PP”ä½»COÓŚE
ČōĖıߊĪPOP”äCŹĒĮāŠĪ£¬ŌņÓŠ![]() £»
£»
Į¬½ÓPP”䣬Ōņ![]() ÓŚE£¬
ÓŚE£¬
”ßC![]() £¬
£¬
”ą![]() £¬
£¬
ÓÖ”ß![]() £¬
£¬
”ą![]() ,
,
”ą![]() £»
£»
”ą![]() £¬
£¬
½āµĆ![]() £¬
£¬![]() £Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬
£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬
”ąPµćµÄ×ų±źĪŖ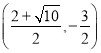 .
.
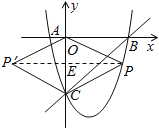
£Ø3£©¹żµćP×÷yÖįµÄĘ½ŠŠĻßÓėBC½»ÓŚµćQ£¬ÓėOB½»ÓŚµćF£¬ÉčPµć×ų±źĪŖ![]() £¬ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖ£ŗ
£¬ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖ£ŗ![]() £¬
£¬
Ōņ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖ![]() £¬
£¬
ŌņQµćµÄ×ų±źĪŖ![]() £»
£»
µ±![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
£½![]()
£½![]()
£½![]()
µ±![]() Ź±£¬ĖıߊĪABPCµÄĆ껿×ī“ó
Ź±£¬ĖıߊĪABPCµÄĆ껿×ī“ó
“ĖŹ±PµćµÄ×ų±źĪŖ![]() £¬ĖıߊĪABPCµÄĆ껿µÄ×ī“óÖµĪŖ
£¬ĖıߊĪABPCµÄĆ껿µÄ×ī“óÖµĪŖ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½©£Øx©m£©2+4£Øm£¾0£©µÄ¶„µćĪŖA£¬ÓėÖ±Ļßx£½![]() Ļą½»ÓŚµćB£¬µćA¹ŲÓŚÖ±Ļßx£½
Ļą½»ÓŚµćB£¬µćA¹ŲÓŚÖ±Ļßx£½![]() µÄ¶Ō³ĘµćĪŖC£®
µÄ¶Ō³ĘµćĪŖC£®
£Ø1£©ČōÅ×ĪļĻßy£½©£Øx©m£©2+4£Øm£¾0£©¾¹żŌµć£¬ĒómµÄÖµ£®
£Ø2£©µćCµÄ×ų±źĪŖ”” ””£®ÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾µćBµ½Ö±ĻßACµÄ¾ąĄėĪŖ”” ””£®
£Ø3£©½«y£½©£Øx©m£©2+4£Øm£¾0£¬ĒŅx”Ż![]() £©µÄŗÆŹżĶ¼Ļó¼ĒĪŖĶ¼ĻóG£¬Ķ¼ĻóG¹ŲÓŚÖ±Ļßx£½
£©µÄŗÆŹżĶ¼Ļó¼ĒĪŖĶ¼ĻóG£¬Ķ¼ĻóG¹ŲÓŚÖ±Ļßx£½![]() µÄ¶Ō³ĘĶ¼Ļó¼ĒĪŖĶ¼ĻóH£®Ķ¼ĻóGÓėĶ¼ĻóH×éŗĻ³ÉµÄĶ¼Ļó¼ĒĪŖĶ¼ĻóM£®
µÄ¶Ō³ĘĶ¼Ļó¼ĒĪŖĶ¼ĻóH£®Ķ¼ĻóGÓėĶ¼ĻóH×éŗĻ³ÉµÄĶ¼Ļó¼ĒĪŖĶ¼ĻóM£®
¢Łµ±Ķ¼ĻóMÓėxÖįĒ”ŗĆÓŠČżøö½»µćŹ±£¬ĒómµÄÖµ£®
¢Śµ±”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬Ö±½ÓŠ“³öĶ¼ĻóMĖł¶ŌÓ¦µÄŗÆŹżÖµŠ”ÓŚ0Ź±£¬×Ō±äĮæxµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŗÆŹż![]() µÄĶ¼Ļó¾¹żŌµć£¬æŖæŚĻņÉĻ£¬¶Ō³ĘÖįĪŖÖ±Ļß
µÄĶ¼Ļó¾¹żŌµć£¬æŖæŚĻņÉĻ£¬¶Ō³ĘÖįĪŖÖ±Ļß![]() £¬¶ŌÓŚĻĀĮŠĮ½øö½įĀŪ£ŗ¢ŁmĪŖČĪŅāŹµŹż£¬ŌņÓŠ
£¬¶ŌÓŚĻĀĮŠĮ½øö½įĀŪ£ŗ¢ŁmĪŖČĪŅāŹµŹż£¬ŌņÓŠ![]() £»¢Ś·½³Ģ
£»¢Ś·½³Ģ![]() ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£¬Ņ»øöøłŠ”ÓŚ0£¬ĮķŅ»øöøł“óÓŚ2£¬Ėµ·ØÕżČ·µÄŹĒ£Ø £©
ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£¬Ņ»øöøłŠ”ÓŚ0£¬ĮķŅ»øöøł“óÓŚ2£¬Ėµ·ØÕżČ·µÄŹĒ£Ø £©
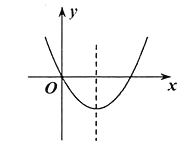
A.¢Ł¶Ō£¬¢Ś“ķB.¢Ł“ķ£¬¢Ś¶ŌC.¢Ł¢Ś¶¼¶ŌD.¢Ł¢Ś¶¼“ķ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬ŅŌABĪŖÖ±¾¶×÷”ŃO£¬½»BC±ßÓŚµćD£¬½»AC±ßÓŚµćF£¬×÷DE”ĶACÓŚµćE£®
£Ø1£©ĒóÖ¤£ŗDEŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”÷ABCµÄ±ß³¤ĪŖ4£¬ĒóEFµÄ³¤¶Č£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
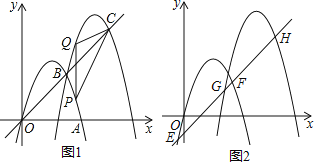
”¾ĢāÄæ”æČēĶ¼1£¬Å×ĪļĻßM1£ŗy£½©x2+4x½»xÕż°ėÖįÓŚµćA£¬½«Å×ĪļĻßM1ĻČĻņÓŅĘ½ŅĘ3øöµ„Ī»£¬ŌŁĻņÉĻĘ½ŅĘ3øöµ„Ī»µĆµ½Å×ĪļĻßM2£¬M1ÓėM2½»ÓŚµćB£¬Ö±ĻßOB½»M2ÓŚµćC£®
£Ø1£©ĒóÅ×ĪļĻßM2µÄ½āĪöŹ½£»
£Ø2£©µćPŹĒÅ×ĪļĻßM1ÉĻAB¼äµÄŅ»µć£¬×÷PQ”ĶxÖį½»Å×ĪļĻßM2ÓŚµćQ£¬Į¬½ÓCP£¬CQ£®ÉčµćPµÄŗį×ų±źĪŖm£¬µ±mĪŖŗĪÖµŹ±£¬Ź¹”÷CPQµÄĆ껿×ī“󣬲¢Ēó³ö×ī“óÖµ£»
£Ø3£©ČēĶ¼2£¬½«Ö±ĻßOBĻņĻĀĘ½ŅĘ£¬½»Å×ĪļĻßM1ÓŚµćE£¬F£¬½»Å×ĪļĻßM2ÓŚµćG£¬H£¬Ōņ![]() µÄÖµŹĒ·ńĪŖ¶ØÖµ£¬Ö¤Ć÷ÄćµÄ½įĀŪ£®
µÄÖµŹĒ·ńĪŖ¶ØÖµ£¬Ö¤Ć÷ÄćµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬E”¢F·Ö±šĪŖ±ßAB”¢CDµÄÖŠµć£¬BDŹĒ¶Ō½ĒĻߣ¬AG”ĪDB½»CBµÄŃÓ³¤ĻßÓŚG£®

£Ø1£©ĒóÖ¤£ŗ”÷ADE”Õ”÷CBF£»
£Ø2£©ČōĖıߊĪ BEDFŹĒĮāŠĪ£¬ŌņĖıߊĪAGBDŹĒŹ²Ć“ĢŲŹāĖıߊĪ£æ²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾Ż±ØµĄ£¬“Ó2018Äź8ŌĀŅŌĄ“”°·ĒÖŽÖķĪĮ”±øųÉśÖķŃųÖ³»§“ųĄ“ĮĖ²»æɹĄĮæµÄĖšŹ§£¬Ä³ŃųÖ³»§ĪŖĮĖŌ¤·Ą”°·ĒÖŽÖķĪĮ”±µÄĒÖĻ®£¬ĆæĢģ¶ŌÖķ³”½ųŠŠŅ©Ń¬Ļū¶¾£¬ŅŃÖŖŅ»ĘæŅ©ĪļŹĶ·Å¹ż³ĢÖŠ£¬Ņ»øöȦÉįÄŚĆæĮ¢·½Ć×æÕĘųÖŠŗ¬Ņ©Įæy£ØŗĮæĖ£©ÓėŹ±¼äx£Ø·ÖÖÓ£©Ö®¼äĀś×ćÕż±ČĄżŗÆŹż¹ŲĻµ£»Ņ©ĪļŹĶ·ÅĶźŗó£¬yÓėxÖ®¼äĀś×ć·“±ČĄżŗÆŹż¹ŲĻµ£¬ČēĶ¼ĖłŹ¾£¬½įŗĻĶ¼ÖŠĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā.
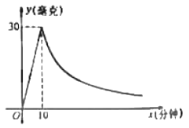
£Ø1£©·Ö±šĒóµ±![]() ŗĶ
ŗĶ![]() Ź±£¬yÓėxÖ®¼äĀś×ćµÄŗÆŹż¹ŲĻµŹ½£»
Ź±£¬yÓėxÖ®¼äĀś×ćµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©¾Ż²ā¶Ø£¬µ±æÕĘųÖŠĆæĮ¢·½Ć×µÄŗ¬Ņ©Įæ²»µĶÓŚ6ŗĮæĖŹ±£¬Ļū¶¾²ÅÓŠŠ§£¬ÄĒĆ“Õā“ĪѬŅ©µÄÓŠŠ§Ļū¶¾Ź±¼äŹĒ¶ąÉŁ·ÖÖÓ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”÷ABCÖŠ£¬AB£½AC£½5cm£¬AB±ßÉĻµÄøßĪŖ3£¬ŌņsinB£½_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
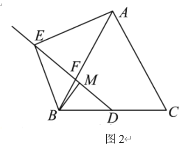
”¾ĢāÄæ”æŅŃÖŖ£ŗŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬µć
£¬µć![]() ĪŖ
ĪŖ![]() ±ßµÄÖŠµć£¬µć
±ßµÄÖŠµć£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬Į¬½Ó
ÉĻ£¬Į¬½Ó![]() ²¢ŃÓ³¤µ½µć
²¢ŃÓ³¤µ½µć![]() £¬Ź¹
£¬Ź¹![]() £¬µć
£¬µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() .
.
£Ø1£©ČēĶ¼1£¬Į¬½Ó![]() £¬µ±
£¬µ±![]() Ź±£¬ĒóÖ¤£ŗ
Ź±£¬ĒóÖ¤£ŗ![]()
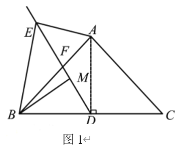
£Ø2£©ČēĶ¼2£¬µ±![]() Ź±£¬ŌņĻ߶Ī
Ź±£¬ŌņĻ߶Ī![]() Ö®¼äµÄŹżĮæ¹ŲĻµĪŖ £»
Ö®¼äµÄŹżĮæ¹ŲĻµĪŖ £»

£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ŃÓ³¤![]() µ½
µ½![]() £¬Ź¹
£¬Ź¹![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬Čō
£¬Čō![]() £¬
£¬![]() £¬ĒóÖ¤£ŗ
£¬ĒóÖ¤£ŗ![]() £¬²¢Ēó
£¬²¢Ēó![]() µÄÕżĻŅÖµ.
µÄÕżĻŅÖµ.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com