
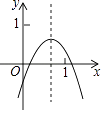
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( ) 
A.2
B.3
C.4
D.5
【答案】C
【解析】解:解:①图象开口向下,与y轴交于负半轴,对称轴在y轴右侧,能得到:a<0,c<0,
∴ac>0,故①正确;②当x=1时,y>0,∴a+b+c>0,故②错误;③当x=﹣2时,y<0,∴4a﹣2b+c<0,故③正确;④∵对称轴x=﹣ ![]() <1,
<1,
∴2a+b>0,故④错误;⑤∵抛物线的顶点在x轴的上方,
∴ ![]() >0,
>0,
∴4ac﹣b2<4a,故⑤正确;⑥∵2a+b>0,
∴2a+b﹣a>﹣a,
∴a+b>﹣a,
∵a<0,
∴﹣a>0,
∴a+b>0,故⑥正确;
综上所述正确的个数为4个,
故选:C.
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠ACB=90°,点F是AB上一点,作等腰Rt△FCP,且∠PCF=90°,连结AP.
(1)求证:△CFB≌△CPA;
(2)求证:AP2+AF2=PF2;
(3)如图2,在AF上取点E,使∠ECF=45°,求证:AE2+BF2=EF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏的中奖概率是 ![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据 8,8,7,10,6,8,9 的众数和中位数都是8
D.若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是![]() .”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
.”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕![]() )的值;
)的值;
(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: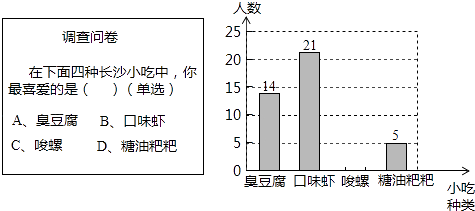
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
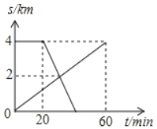
A. 8:30 B. 8:35 C. 8:40 D. 8:45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com