
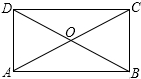
 如图,在矩形ABCD中,对角线AC,BD相交于O,∠AOB=120°,AD=3,那么对角线AC的长是6.
如图,在矩形ABCD中,对角线AC,BD相交于O,∠AOB=120°,AD=3,那么对角线AC的长是6.  小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
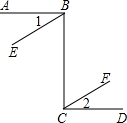 如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程
如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
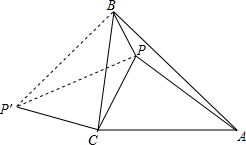 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com