
【题目】如图,四边形ABCD中,AC=5,AB=4,CD=12,AD=13,∠B=90°.
(1)求BC边的长;
(2)求四边形ABCD的面积.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 边的中点,过点
边的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:四边形
,求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,当
,当![]() 时,取
时,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形
,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车分别从A市和B市两地同时出发,匀速行驶,先相向而行,慢车到达A市后停止行驶,快车到达B市后,立即按原路原速度返回A市(调头时间忽略不计),结果与慢车同时到达A市.快、慢两车距B市的路程y1、y2(单位:km)与出发时间x(单位:h)之间的函数图像如图所示.
(1)A市和B市之间的路程是 km;
(2)求a的值,并解释图中点M的横坐标、纵坐标的实际意义;
(3)快车与慢车迎面相遇以后,再经过多长时间两车相距20 km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)问题探究:线段OB,OC有何数量关系,并说明理由;
(2)问题拓展:分别连接OA,BC,试判断直线OA,BC的位置关系,并说明理由;
(3)问题延伸:将题目条件中的“CD⊥AB于D,BE⊥AC于E”换成“D、E分别为AB,AC边上的中点”,(1)(2)中的结论还成立吗?请直接写出结论,不必说明理由.
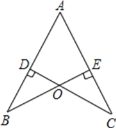
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列五个结论:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,则
;③ON⊥OM;④若AB=2,则![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正确结论是_________.(只填番号)
.其中正确结论是_________.(只填番号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用5500元购进甲、乙两种矿泉水共180箱,矿泉水的成本价与销售价如下表所示:
类别 | 成本价(元 | 销售价(元 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这180箱矿泉水,可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com