
����Ŀ����ͼ����һ����������ת����ת���У�ָ��λ�ù̶����������ε��������ȣ��ҷֱ��������1��2��3��
��1��С��ת��ת��һ�Σ���ת��ֹͣת��ʱ��ָ����ָ�����е������������ĸ���Ϊ�� ����
��2��С����ת��ת��һ�Σ���ת��ֹͣת��ʱ����¼��ָ����ָ�����е����֣�������ת��ת��һ�Σ���ת��ֹͣת��ʱ���ٴμ�¼��ָ����ָ�����е����֣�������������֮����3�ı����ĸ��ʣ��û���״ͼ���б��ȷ�����⣩��

���𰸡���1��![]() ����2����������
����2����������![]()
��������
��1���ɱ�������1��2��3��3��ת���У���������1��3��2�������ø��ʹ�ʽ����ɵã�
��2�����������б��ó����еȿ��ܵ���������ó�����������֮����3�ı�������������ٸ��ݸ��ʹ�ʽ���ɵó��𰸣�
��1�����ڱ�������1��2��3��3��ת���У���������1��3��2����
��ָ����ָ�����е������������ĸ���Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���б����£�
1 | 2 | 3 | |
1 | (1��1) | (2��1) | (3��1) |
2 | (1��2) | (2��2) | (3��2) |
3 | (1��3) | (2��3) | (3��3) |
�ɱ���֪�����еȿ��ܵ������Ϊ9�֣���������������֮����3�ı�������3�֣�
��������������֮����3�ı����ĸ���Ϊ![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ��
��![]() �ύ��A��B���㣨��A�ڵ�B��ࣩ
�ύ��A��B���㣨��A�ڵ�B��ࣩ
��1���������ߵĶ������꣨�ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2�����߶�AB�ij���
��3����������![]() �ύ�ڵ�C����C����ԭ��
�ύ�ڵ�C����C����ԭ��![]() �غϣ�����
�غϣ�����![]() �����ʼ��С��
�����ʼ��С��![]() ���������
���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����عذ�����ѧ����ijѧУ������ѧ���ĸ������ηֳ��������ͣ�A���ɸ�ĸһ���տ���B����үү�����տ���C�������̵Ƚ����տ���D��ֱ�Ӽ���ѧУ��ij��ѧС�����������һ���༶�����ָð�����ѧ������ռȫ����������20%�������������Ƴ�����������������ͳ��ͼ��
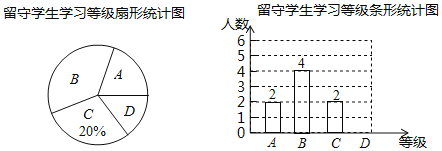
��1���ð���� ��������ѧ����B��������ѧ���������ε�Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ����������
��3����֪��У����2400��ѧ������ѧУ�����D���͵�����ѧ�����������ֹذ����������Ƹ�У���ж���������ѧ���ڴ˹ذ�������棿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
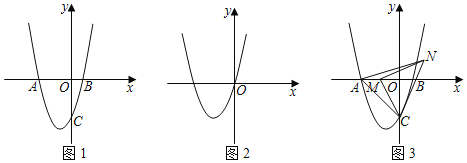
����Ŀ����֪��ƽ��ֱ������ϵ�У�������y��x2+3x��a2+a+2��a��1����ͼ��x���ڵ�A�͵�B����A�ڵ�B��ࣩ����y�ύ�ڵ�C������ΪE��
��1����ͼ1�����߶�AB�ij��ȣ��ú�a��ʽ�ӱ�ʾ���������ߵĶԳ��
��2����ͼ2���������ߵ�ͼ��ԭ��ʱ����ƽ�����Ƿ����һ��P��ʹ����A��B��E��PΪ������ı����ܷ��Ϊƽ���ı��Σ�����ܣ����P�����ꣻ������ܣ���˵�����ɣ�
��3����ͼ3����a��3ʱ����M��Ϊx����һ���㣬����MC�����߶�MC�Ƶ�M��ʱ����ת90��õ��߶�MN������AC��CN��AN�����ACN�ܳ�����СֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��OAB�У���OAB=90������BOA=30����OA=2![]() ������OΪ����ԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����
������OΪ����ԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����

��1������O��C��A����������ߵĽ���ʽ��
��2������M����������һ�㣬��λ���߶�OC���Ϸ�������MO��MC���ʣ���Mλ�ںδ�ʱ������MOC�����������������MOC����������
��3�����������Ƿ����һ��P��ʹ��OAP=��BOC�������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
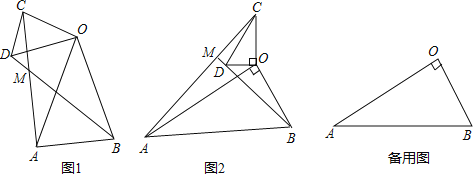
��ͼ1������OAB����OCD�У�OA=OB��OC=OD����AOB=��COD=40��������AC��BD���ڵ�M����գ�
��![]() ��ֵΪ�� ����
��ֵΪ�� ����
�ڡ�AMB�Ķ���Ϊ�� ����
��2�����̽��
��ͼ2������OAB����OCD�У���AOB=��COD=90�㣬��OAB=��OCD=30��������AC��BD���ӳ����ڵ�M�����ж�![]() ��ֵ����AMB�Ķ�������˵�����ɣ�
��ֵ����AMB�Ķ�������˵�����ɣ�
��3����չ����
�ڣ�2���������£�����OCD�Ƶ�O��ƽ������ת��AC��BD����ֱ�߽��ڵ�M����OD=1��OB=![]() ����ֱ��д������C���M�غ�ʱAC�ij���
����ֱ��д������C���M�غ�ʱAC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������Ϊ6ǧ�Ĺ���![]() ������
������![]() ��
��![]() �������ӳ���·�ֱ�������·���ӣ����ӵ�Ϊ
�������ӳ���·�ֱ�������·���ӣ����ӵ�Ϊ![]() ��
��![]() ������
������![]() ��
��![]() ֮��ľ���Ϊ2ǧ�ף�
֮��ľ���Ϊ2ǧ�ף�![]() ��
��![]() ֮��ľ���Ϊ1ǧ�ף�
֮��ľ���Ϊ1ǧ�ף�![]() ��
��![]() ֮�������·����Ϊ2.3ǧ�ף�
֮�������·����Ϊ2.3ǧ�ף�![]() ��
��![]() ֮�������·����Ϊ3.2ǧ�ף�Ϊ�˷�չ���ã���������������������ͣ�����Ҫ�ڹ���
֮�������·����Ϊ3.2ǧ�ף�Ϊ�˷�չ���ã���������������������ͣ�����Ҫ�ڹ���![]() ����һ����������
����һ����������![]() ����
����![]() ��
��![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ǧ�ף���������
ǧ�ף���������![]() �ع�·��
�ع�·��![]() ��
��![]() ��������ľ���֮��Ϊ
��������ľ���֮��Ϊ![]() ���ף������ǶԺ���
���ף������ǶԺ���![]() ���Ա���
���Ա���![]() �ı仯���ɽ��е�̽�����벹��������
�ı仯���ɽ��е�̽�����벹��������
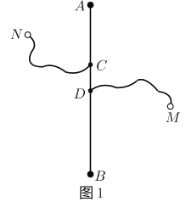
��1��ͨ��ȡ�㡢��ͼ���������õ�![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
��2����ͼ2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����ϻ����ĺ���ͼ������⣺
����Ҫʹ��������![]() �ع�·��
�ع�·��![]() ��
��![]() ��������ľ���֮����С������������
��������ľ���֮����С������������![]() Ӧ�����ںδ�����д����������������λ�ã�
Ӧ�����ںδ�����д����������������λ�ã�
��__________��
������ͼ�����ĸ�����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ�λ�ڹ���
�ֱ�λ�ڹ���![]() ���࣬�ӳ���·�ֱ�������·���ӣ���Ҫ�ڹ�������һ����������
���࣬�ӳ���·�ֱ�������·���ӣ���Ҫ�ڹ�������һ����������![]() ��ʹ��
��ʹ��![]() �ع�·��
�ع�·��![]() ��
��![]() ��
��![]() ��
��![]() �ľ���֮����С������������
�ľ���֮����С������������![]() Ӧ�����ںδ�����д����������������λ�ã�
Ӧ�����ںδ�����д����������������λ�ã�
��__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�Ӫһ��ˮ���꣬ij�յ�ˮ�������г�����һ��ˮ�������˽⣬һ������������ˮ����������![]() ������
������![]() ʱ����������ˮ�����������۾�Ϊ3Ԫ
ʱ����������ˮ�����������۾�Ϊ3Ԫ![]() ��ͼ�����߱�ʾ��������
��ͼ�����߱�ʾ��������![]() ��Ԫ
��Ԫ![]() ��������
��������![]() �ĺ�����ϵ��
�ĺ�����ϵ��
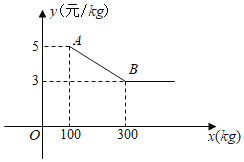
��1����ͼ���߶�![]() ����ֱ�ߵĺ�������ʽ��
����ֱ�ߵĺ�������ʽ��
��2��С����800Ԫһ�ο�����������ˮ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�AB��AC��AB=![]() ��BC=
��BC=![]() ,�Խ���AC��BD�ཻ�ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F,����˵����������ת�����У�AF=CE. ��OB=AC��������ת�����У��ı���ABEF�����Ϊ
,�Խ���AC��BD�ཻ�ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F,����˵����������ת�����У�AF=CE. ��OB=AC��������ת�����У��ı���ABEF�����Ϊ![]() ���ܵ�ֱ��AC�Ƶ�O˳ʱ����ת30��ʱ������BF,DE���ı���BEDF�����Σ�������ȷ���ǣ� ��
���ܵ�ֱ��AC�Ƶ�O˳ʱ����ת30��ʱ������BF,DE���ı���BEDF�����Σ�������ȷ���ǣ� ��
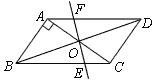
A.�٢ڢ�B.�� ��C.�٢ڢۢ�D.�� �� ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com