
分析 根据直角三角形30°角所对的直角边等于斜边的一半,然后根据勾股定理列方程求出BD的值,即可得解.
解答 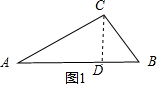 解:如图1,过点C作CD⊥BA于D,设CD=x,
解:如图1,过点C作CD⊥BA于D,设CD=x,
∵∠A=30°,
∴AC=2x,AD=$\sqrt{3}$x,
∵AC=$\sqrt{3}$,
∴x=$\frac{\sqrt{3}}{2}$,
∴CD=$\frac{\sqrt{3}}{2}$,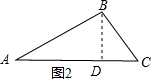
∴BD=$\frac{1}{2}$,
∴AB=2,
如图2.过B作BD⊥AC于D,
∵∠A=30°,
∴AB=$\frac{1}{2}$BD,AD=$\sqrt{3}$BD,
∴CD=$\sqrt{3}$-$\sqrt{3}$BD,
∵BC=1,
在Rt△BCD中,BD2+CD2=BC2,
即BD2+($\sqrt{3}$-$\sqrt{3}$BD)2=12,
解得
所以,DB=1或$\frac{1}{2}$.
∴AB=1.或AB=2,
故答案为:1或2.
点评 本题考查了解直角三角形,直角三角形30°角所对的直角边等于斜边的一半,勾股定理,作辅助线构造出两个直角三角形是解题的关键,作出图形更形象直观.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
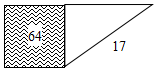 如图,阴影部分是一个面积为64的正方形,以它的一边为直角边作斜边长为17的直角三角形,这个直角三角形的另一条直角边长为( )
如图,阴影部分是一个面积为64的正方形,以它的一边为直角边作斜边长为17的直角三角形,这个直角三角形的另一条直角边长为( )| A. | 9 | B. | 15 | C. | 47 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
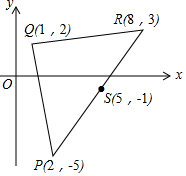 图中的P(2,-5),Q(1,2)和R(8,3)是一个三角形的顶点
图中的P(2,-5),Q(1,2)和R(8,3)是一个三角形的顶点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
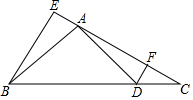 如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.
如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:| 组别 | 成绩(分) | 频数 |
| A | 50≤x<60 | 6 |
| B | 60≤x<70 | m |
| C | 70≤x<80 | 20 |
| D | 80≤x<90 | 36 |
| E | 90≤x<100 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com