
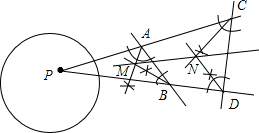
 �Ķ�������ϣ�
�Ķ�������ϣ����� �������������������������ڽǵ�ƽ�����ཻ��һ�����жϡ�P��ƽ���߹���M��������ͬ�������жϡ�P��ƽ���߱ع���N����������ȷ��һ��ֱ�߿��ж�ֱ��MNƽ�֡�P��
��� �⣺�������õ�MΪ��PAB�Ľ�ƽ���ߵĽ��㣬���������������ڽǵ�ƽ�����ཻ��һ�㣬���P��ƽ���߱ع���M��
ͬ������NΪ��PCD�Ľ�ƽ���ߵĽ��㣬���P��ƽ���߱ع���N��
����ֱ��MNƽ�֡�P��
�ʴ�Ϊ�����������ڽǵ�ƽ�����ཻ��һ�㣻����ȷ��һ��ֱ�ߣ�
���� ���⿼���˻�����ͼ������5��������ͼ����һ���߶ε�����֪�߶Σ���һ���ǵ�����֪�ǣ�����֪�߶εĴ�ֱƽ���ߣ�����֪�ǵĽ�ƽ���ߣ���һ������ֱ֪�ߵĴ��ߣ�����Ҳ��ʾ�˻���ƽ�е���һ�ַ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AO=CO��BO=DO���ҡ�ABC+
��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AO=CO��BO=DO���ҡ�ABC+�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
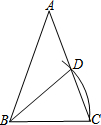 ��ͼ���ڡ�ABC�У�AB=AC����A=36�㣬��BΪԲ�ģ�BCΪ�뾶��������AC�ڵ�D������BD�����ABD=36�㣮
��ͼ���ڡ�ABC�У�AB=AC����A=36�㣬��BΪԲ�ģ�BCΪ�뾶��������AC�ڵ�D������BD�����ABD=36�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
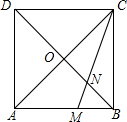 ��ͼ��������ABCD�ı߳�Ϊ3���Խ���AC��BD�ཻ�ڵ�O��CM��BD�ڵ�N����BM=1�����߶�ON�ij�Ϊ$\frac{3\sqrt{2}}{4}$��
��ͼ��������ABCD�ı߳�Ϊ3���Խ���AC��BD�ཻ�ڵ�O��CM��BD�ڵ�N����BM=1�����߶�ON�ij�Ϊ$\frac{3\sqrt{2}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
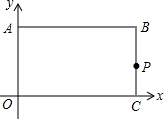 ��ͼ������ABCO��OΪ����ԭ�㣬B������Ϊ��8��6����A��C�ֱ����������ϣ�P���߶�BC�϶��㣬��PC=m����֪��D�ڵ�һ���ޣ�����ֱ��y=2x-6���ϵ�һ�㣮����APD�ǵ���Rt�������D������Ϊ��4��2����$\frac{20}{3}$��$\frac{22}{3}$����$\frac{28}{3}$��$\frac{38}{3}$����
��ͼ������ABCO��OΪ����ԭ�㣬B������Ϊ��8��6����A��C�ֱ����������ϣ�P���߶�BC�϶��㣬��PC=m����֪��D�ڵ�һ���ޣ�����ֱ��y=2x-6���ϵ�һ�㣮����APD�ǵ���Rt�������D������Ϊ��4��2����$\frac{20}{3}$��$\frac{22}{3}$����$\frac{28}{3}$��$\frac{38}{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
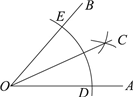 | ����������OΪԲ�ģ����ⳤΪ�뾶��������OA��OB�ڵ�D��E�� �ڷֱ���D��EΪԲ�ģ��Դ���$\frac{1}{2}$DE�ij�Ϊ�뾶�����������ڡ�AOB�ڽ��ڵ�C�� ��������OC����OC���ǡ�AOB��ƽ���ߣ� |
| A�� | SSS | B�� | SAS | C�� | ASA | D�� | AAS |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ڷ���ȷ�� | B�� | �Գ���λ��ȷ�� | ||
| C�� | ��y��Ľ���һ���������� | D�� | ��x��Ľ���һ����һ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x | B�� | $\frac{1}{x}$ | C�� | $\frac{x+1}{x-1}$ | D�� | $\frac{x-1}{x+1}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com