
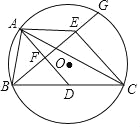
【题目】如图,△ABC内接于⊙O,AD是△ABC的中线,AE∥BC,射线BE交AD于点F,交⊙O于点G,点F是BE的中点,连接CE.
(1)求证:四边形ADCE为平行四边形;
(2)若BC=2AB,求证: ![]() .
.
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 两点,且与y轴交于点C.
两点,且与y轴交于点C.

(1)求抛物线的表达式;
(2)如图①,在抛物线的对称轴上寻找一点M,使得△ACM的周长最小,求点M的坐标.
(3)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P,Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP,DQ.若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D的坐标;
,求△DPQ面积的最大值,并求此时点D的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步促进“美丽校园”创建工作,某校团委计划对八年级五个班的文化建设进行检查,每天随机抽查一个班级,第一天从五个班级随机抽取一个进行检查,第二天从剩余的四个班级再随机抽取一个进行检查,第三天从剩余的三个班级再随机抽取一个进行检查…,以此类推,直到检查完五个班级为止,且每个班级被选中的机会均等
(1)第一天,八(1)班没有被选中的概率是 ;
(2)利用网状图或列表的方法,求前两天八(1)班被选中的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
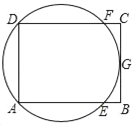
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法,其中正确说法的个数是( )
(1)AC与BD的交点是圆O的圆心;
(2)AF与DE的交点是圆O的圆心;
(3)![]() ;
;
(4)DE>DG,
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进城乡生活垃圾分类的行动中,某校数学兴趣小组为了了解居民掌握垃圾分类知识的情况,对![]() 两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
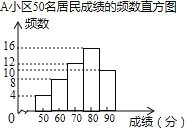
(信息二)上图中,从左往右第四组成绩如下:
75 | 77 | 77 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | ___________ | 79 | 40% | 277 |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区600名居民成绩能超过平均数的人数;
小区600名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,选择合适的统计量分析![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com