
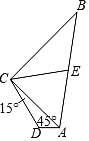
【题目】已知四边形ABCD中,AB=10,BC=8,CD=![]() ∠DAC=45°,∠DCA=15°.
∠DAC=45°,∠DCA=15°.
(1)求△ADC的面积;
(2)若E为AB的中点,求线段CE的长。
【答案】(1)![]() ;(2)CE=5.
;(2)CE=5.
【解析】
(1)过点C作CF⊥AD,交AD延长线于点F,构造含有30度角的直角△CFD,通过解该直角三角形求得DF、CF的长度,进而利用等腰直角△ACF的性质求得AD的长度,结合三角形的面积公式解答即可;
(2)由勾股定理的逆定理得到△ABC是直角三角形,由“直角三角形斜边上的中线等于斜边的一半”解答.
(1)过点C作CF⊥AD,交AD延长线于点F,
∵∠DAC=45°,∠DCA=15°,
∴∠CDF=∠DAC+∠DCA=45°+15°=60°,
在Rt△CFD中,CD=2![]() ,
,
∴DF=![]() CD=
CD=![]() ,CF=
,CF=![]() ,
,
∴AD=AFDF=3![]() ,
,
∴S△ADC=![]() AD×CF=
AD×CF=![]() ×(2
×(2![]()
![]() )×3
)×3![]() =93
=93![]() .
.
(2)在Rt△AFC中,∵∠DAC=45°,CF=3![]() ,
,
∴AC=![]() CF=
CF=![]() ×3
×3![]() =6,
=6,
在△ABC中,∵AC2+BC2=62+82=AB2
∴△ABC是直角三角形,
又∵E为AB中点,
∴CE=![]() AB=
AB=![]() ×10=5.
×10=5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把下列各数分别填在相应的集合里:
![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,……
,……
正有理数集合:{ …}
整数集合:{ …}
分数集合:{ …}
(2)在下面的数轴上表示下列各数,并按照从小到大的顺序用“<”号连接起来
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司销售部门提供了某种产品销售收入(记为: ![]() /元)、销售成本(记为:
/元)、销售成本(记为:![]() /元)、销售量(记为:
/元)、销售量(记为: ![]() /吨)方面的信息如下:
/吨)方面的信息如下:
①![]() 时,
时,![]() ;
;
②![]() 时,
时,![]()
![]() ;
;
③![]() 与
与![]() 成正比例函数关系;④
成正比例函数关系;④![]() 与
与![]() 成一次函数关系.
成一次函数关系.
依据上述信息,解决下列问题:
(1)分别求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)销售量为多少吨时,销售收入与销售成本相同?
(3)若销售量为![]() 吨时,求公司的利润. (利润=销售收入-销售成本)
吨时,求公司的利润. (利润=销售收入-销售成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[材料阅读]
材料一:如图,![]() ,点
,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() ,点
,点![]() ,D分别在
,D分别在![]() 上.可求得如下结论:
上.可求得如下结论:![]() ,
,![]() 为定值.
为定值.
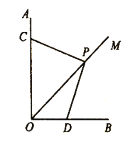
材料二(性质):四边形的内角和为![]() .
.
[问题解决]
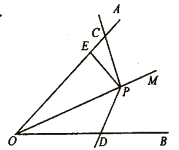
(1)如图,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() 的边与
的边与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
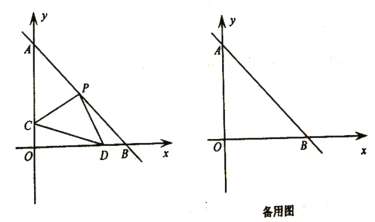
(2)如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,连接
,连接![]() .求
.求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某专卖店销售某品牌服装,设服装进价为80元,当每件服装售价为240元时,月销售为200件,该专卖店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每件价格每下降10元时,月销售量就会增加20件,设每件服装售价为x(元),该专卖店的月利润为y(元).
(1)求出y与x的函数关系式(不要求写出x的取值范围);
(2)该专卖店要获得最大月利润,售价应定为每件多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.
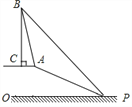
求:(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
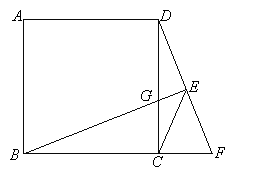
【题目】在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
(1)若正方形ABCD边长为3,DF=4,求CG的长;
(2)求证:EF+EG=![]() CE.
CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
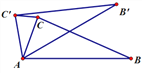
A. 70° B. 35° C. 40° D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com