
【题目】完成下列证明过程. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,说明ED=EF.
解:∵∠DEC=∠B+∠BDE (),
又∵∠DEF=∠B(已知),
∴∠=∠(等式性质).
在△EBD与△FCE中,
∠=∠(已证),
=(已知),
∠B=∠C(已知),
∴△EBD≌△FCE().
∴ED=EF ().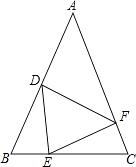
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE , 若∠CAE=65°,∠E=70°,且AD⊥BC , 则∠BAC的度数为( )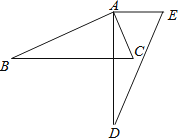
A.60°
B.85°
C.75°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有一个△DEF .
①作△DEF关于直线HG的轴对称图形;
②作△DEF的EF边上的高;
③若网格上的最小正方形边长为1,求△DEF的面积.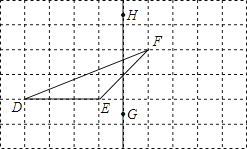
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.

(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上网流量、语音通话是手机通信消费的两大主体,目前,某通信公司推出消费优惠新招﹣﹣“定制套餐”,消费者可根据实际情况自由定制每月上网流量与语音通话时间,并按照二者的阶梯资费标准缴纳通信费.下表是流量与语音的阶梯定价标准.


【小提示:阶梯定价收费计算方法,如600分钟语音通话费=0.15×500+0.12×(600﹣500)=87元】
(1)甲定制了600MB的月流量,花费48元;乙定制了2GB的月流量,花费120.4元,求a,b的值.(注:1GB=1024MB)
(2)甲的套餐费用为199元,其中含600MB的月流量;丙的套餐费用为244.2元,其中包含1GB的月流量,二人均定制了超过1000分钟的每月通话时间,并且丙的语音通话时间比甲多300分钟,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级进行了一次诗歌朗诵比赛,甲、乙两组学生的成绩如表所示:
组别 | 平均分 | 中位数 | 方差 |
甲 | 6.9 | 8 | 2.65 |
乙 | 7.1 | 7 | 0.38 |
你认为哪一组的成绩更好一些?并说明理由.
答:组(填“甲”或“乙”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn=![]() (其中a,b是常数,n≥4)
(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5= ;
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com