
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )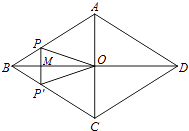
A.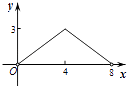
B.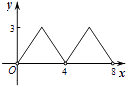
C.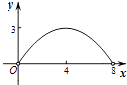
D.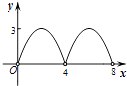
【答案】D
【解析】解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA= ![]() AC=3,OB=
AC=3,OB= ![]() BD=4,AC⊥BD,
BD=4,AC⊥BD,
①当BM≤4时,
∵点P′与点P关于BD对称,
∴P′P⊥BD,
∴P′P∥AC,
∴△P′BP∽△CBA,
∴ ![]() ,即
,即 ![]() ,
,
∴PP′= ![]() x,
x,
∵OM=4﹣x,
∴△OPP′的面积y= ![]() PP′OM=
PP′OM= ![]() ×
× ![]() x(4﹣x)=﹣
x(4﹣x)=﹣ ![]() x2+3x;
x2+3x;
∴y与x之间的函数图象是抛物线,开口向下,过(0,0)和(4,0);
②当BM≥4时,y与x之间的函数图象的形状与①中的相同,过(4,0)和(8,0);
综上所述:y与x之间的函数图象大致为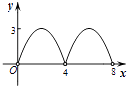 .
.
故选:D.
由菱形的性质得出AB=BC=CD=DA,OA= ![]() AC=3,OB=
AC=3,OB= ![]() BD=4,AC⊥BD,分两种情况:
BD=4,AC⊥BD,分两种情况:
①当BM≤4时,先证明△P′BP∽△CBA,得出比例式 ![]() ,求出PP′,得出△OPP′的面积y是关于x的二次函数,即可得出图象的情形;
,求出PP′,得出△OPP′的面积y是关于x的二次函数,即可得出图象的情形;
②当BM≥4时,y与x之间的函数图象的形状与①中的相同;即可得出结论.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2 .
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2 , 求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;
(2)画出该函数的图象;
(3)判断点(3,5)是否在此函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A第,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
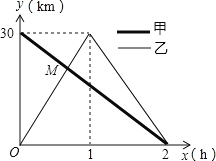
(1)A、B两地之间的距离: km;
(2)甲的速度为 km/h;乙的速度为30km/h;
(3)点M的坐标为 ;
(4)求:甲离B地的距离y(km)与行驶时间x(h)之间的函数关系式(不必写出自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP.
(1)判断四边形CODP的形状并说明理由;
(2)如图②,如果题目中的矩形变为菱形,判断四边形CODP的形状并说明理由;
(3)如图③,如果题目中的矩形变为正方形,判断四边形CODP的形状并说明理由.
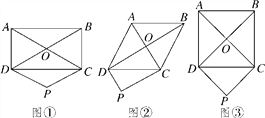
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把成绩结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: 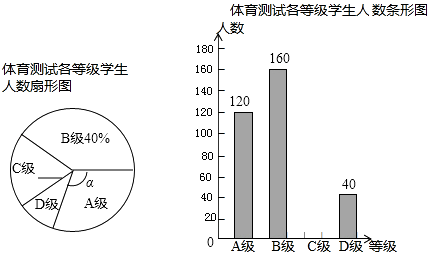
(1)求本次抽样测试的学生人数;
(2)求扇形图中∠α的度数,并把条形统计图补充完整;
(3)该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com