分析:(1)根据弦切角定理得出∠PAB=∠BPE,利用切线长定理得出EP=EC,再利用三角形的外角性质得出∠CPD=∠EPC+∠BPE,即可得出答案;
(2)首先得出△O1PA∽△O2DP,求出AP的长,进而得出BC的长,再利用△DPC∽△CPB,△APC∽△ACD,即可得出PC,CD的关系即可得出PC的长.
解答:
(1)证明:如图1,过点P作两圆的公切线PE,交BC于点E,
∵⊙O
1与⊙O
2外切于点P,直线AC切⊙O
2于点C,
∴EP=EC,∠PAB=∠BPE,
∴∠ECP=∠EPC,
又∵∠PAC+∠ACP=∠CPD,
∴∠CPD=∠EPC+∠BPE,
∴∠BPC=∠CPD;
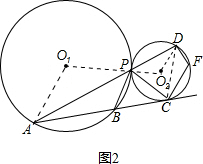
(2)解:如图2,连接O
1O
2,AO
1,DO
2,CD,
∵∠O
1PA=∠O
1AP,∠O
2DP=∠O
2PD,∠O
1PA=∠O
2PD,
∴∠O
1PA=∠O
1AP=∠O
2DP=∠O
2PD,
∴△O
1PA∽△O
2DP,
∴
=
=
,
∵PD=10,
∴AP=20,
∵直线AC切⊙O
2于点C,
∴AC
2=AP×AD=(20+10)×20=600,
∴AC=10
,
∵AB=7
,
∴BC=3
,
∵直线AC切⊙O
2于点C,
∴∠PDC=∠PCB,
∵∠PDC=∠BPC,
∴△DPC∽△CPB,
∴
=
,
∴
=
,
∵∠CAP=∠DAC,∠PCA=∠CDA,
∴△APC∽△ACD,
∴
=
=
=
,
∴CD=
PC,
∴
=
,
解得:PC=2
.
点评:此题主要考查了圆的综合应用以及弦切角定理和相似三角形的性质和判定,根据已知得出PC与CD的比例关系是解题关键.

 (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D. (1)证明:如图1,过点P作两圆的公切线PE,交BC于点E,
(1)证明:如图1,过点P作两圆的公切线PE,交BC于点E,


 (1997•南京)已知如图,在△ABC的外接圆中,D是弧BC的中点,AD交BC于点E,∠ABC的平分线交AD于点F.
(1997•南京)已知如图,在△ABC的外接圆中,D是弧BC的中点,AD交BC于点E,∠ABC的平分线交AD于点F.