

 =2,得到BE=2AE,再利用勾股定理可计算出AE=
=2,得到BE=2AE,再利用勾股定理可计算出AE=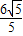 ,则BE=
,则BE=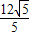 ,在Rt△APC中运用同样的方法得到CP=2AP=2x,AC=
,在Rt△APC中运用同样的方法得到CP=2AP=2x,AC= x,则CE=AC-AE=
x,则CE=AC-AE= x-
x-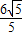 ,再利用∠BAD=∠BCA可证得Rt△APD∽Rt△CEB,根据相似的性质得到
,再利用∠BAD=∠BCA可证得Rt△APD∽Rt△CEB,根据相似的性质得到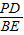 =
= ,即
,即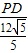 =
=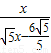 ,即可求出AD.
,即可求出AD. 过B点作BE⊥AC于点E,
过B点作BE⊥AC于点E,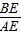 =2,
=2, ,
,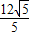 ,
,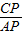 =2,
=2,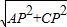 =
=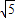 x,
x,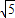 x-
x-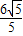 ,
,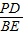 =
=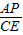 ,即
,即 =
=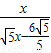 ,
,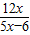 .
.

科目:初中数学 来源: 题型:
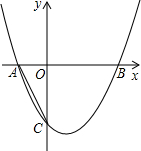 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A,B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且tan∠ACO=
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A,B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且tan∠ACO=| 1 |
| 2 |
| A、此抛物线的解析式为y=x2+x-2 | ||
| B、在此抛物线上的某点M,使△MAB的面积等于4,这样的点共有三个 | ||
C、此抛物线与直线y=-
| ||
| D、当x>0时,y随着x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 点A、B重合).过点P作AB的垂线交射线AM于点C,连接BC,作射线AD交射线CP于点D,且使得∠BAD=∠BCA,设AP=x
点A、B重合).过点P作AB的垂线交射线AM于点C,连接BC,作射线AD交射线CP于点D,且使得∠BAD=∠BCA,设AP=x查看答案和解析>>
科目:初中数学 来源:2011年黑龙江省哈尔滨市南岗区中考数学一模试卷(解析版) 题型:解答题
 时,求t值.
时,求t值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com