
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的角度为________.
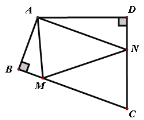
【答案】140°
【解析】
作点A关于BC的对称点A′,关于CD的对称点A″,根据轴对称确定最短路线问题,连接A′A″与BC、CD的交点即为所求的点M、N,利用三角形的内角和定理列式求出∠A′+∠A″,再根据轴对称的性质和三角形的一个外角等于与它不相邻的两个内角的和可得∠AMN+∠ANM=2(∠A′+∠A″),然后计算即可得解.
如图,作点A关于BC的对称点A′,关于CD的对称点A″,连接A′A″与BC、CD的交点即为所求的点M、N.
∵∠BAD=110°,∠B=∠D=90°,∴∠A′+∠A″=180°﹣110°=70°,由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,∴∠AMN+∠ANM=2(∠A′+∠A″)=2×70°=140°.
故答案为:140°.


科目:初中数学 来源: 题型:
【题目】阅读材料:我们都知道,![]()
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为![]() ,所以
,所以![]() ,
,![]()
所以,-2x2+40x+5有最大值205.
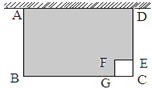
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是 . 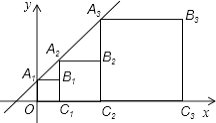
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表 | |||||
项目 | 篮球 | 足球 | 乒乓球 | 排球 | 羽毛球 |
人数 | a | 6 | 5 | 7 | 6 |
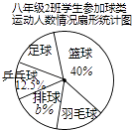
根据图中提供的信息,解答下列问题:
(1)a= , b=;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)在Rt△ABC中,∠C=90°,AB=5cm.BC=a cm,AC=3cm,且a是方程x2﹣(m﹣1)x+m+4=0的根.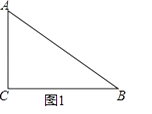
(1)求a和m的值;
(2)如图(2),有一个边长为 ![]() 的等边三角形DEF从C出发,以1cm/s的速度沿CB方向移动,至△DEF全部进入与△ABC为止,设移动时间为xs,△DEF与△ABC重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;
的等边三角形DEF从C出发,以1cm/s的速度沿CB方向移动,至△DEF全部进入与△ABC为止,设移动时间为xs,△DEF与△ABC重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;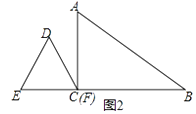
(3)试求出发后多久,点D在线段AB上?
查看答案和解析>>
科目:初中数学 来源: 题型:
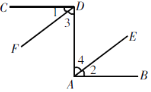
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2. 试说明DF∥AE. 请你完成下列填空,把解答过程补充完整.
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°( ).
∴∠CDA=∠DAB(等量代换).
又∠1=∠2,
从而∠CDA-∠1=∠DAB-________(等式的性质).
即∠3=_______.
∴DF∥AE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com