
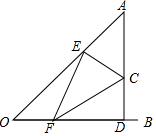
 如图,∠AOB=45°,点C在∠AOB内部,CD⊥OB于点D,CD=5,OD=13,点E、点F分别是射线OA、射线OB上的动点,那么FE+FC的最小值是9$\sqrt{2}$.
如图,∠AOB=45°,点C在∠AOB内部,CD⊥OB于点D,CD=5,OD=13,点E、点F分别是射线OA、射线OB上的动点,那么FE+FC的最小值是9$\sqrt{2}$. 分析 如图,作点E关于OD的对称点E′,作射线OE′,作CE″⊥OE′交OD于F′,延长DC交OA于H,作CM⊥OA于M.因为EF+CF=E′F+CF,所以根据垂线段最短可知,当CE″⊥OE′时,EF+CF的值最小,最小值为CE″,求出CE″即可解决问题.
解答 解:如图,作点E关于OD的对称点E′,作射线OE′,作CE″⊥OE′交OD于F′,延长DC交OA于H,作CM⊥OA于M.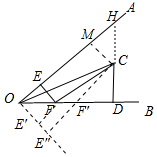
∵EF+CF=E′F+CF,
∴根据垂线段最短可知,当CE″⊥OE′时,EF+CF的值最小,最小值为CE″,
∵∠AOD=45°,∠ADO=90°,
∴∠DOH=∠DHO=45°,
∴OD=DH=13,∵CD=5,
∴CH=8,
∵CM⊥OA,
∴∠CMH=90°,∠MCH=∠MHC=45°,
∴CM=MH=4$\sqrt{2}$,
∵∠AOE′=2∠AOD=90°=∠OE″C=∠CMO,
∴四边形CMOE″是矩形,
∴OE″=CM=4$\sqrt{2}$,
在Rt△OCD中,OC2=OD2+CD2=132+52=194,
在Rt△OCE″中,CE″=$\sqrt{O{C}^{2}-OE{″}^{2}}$=$\sqrt{194-32}$=9$\sqrt{2}$,
∴EF+CF的值最小为9$\sqrt{2}$.
故答案为9$\sqrt{2}$.
点评 本题考查轴对称-最短问题,等腰直角三角形的性质、勾股定理、矩形的性质等知识,解题的关键是学会利用对称,垂线段最短解决最小值问题,灵活运用勾股定理,所以中考常考题型.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:填空题
 小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.
小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
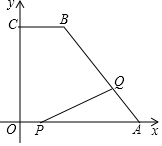 如图,在平面直角坐标系中,已知点A(10,0),B(4,8)C(0,8),连接AB,BC,点P从坐标原点O出发,以每秒1个单位长度的速度向点A运动,同时,点Q从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,当其中一点到达终点时,另一点也随之停止运动,设两点运动的时间为t秒,请解答下列问题:
如图,在平面直角坐标系中,已知点A(10,0),B(4,8)C(0,8),连接AB,BC,点P从坐标原点O出发,以每秒1个单位长度的速度向点A运动,同时,点Q从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,当其中一点到达终点时,另一点也随之停止运动,设两点运动的时间为t秒,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com