
【题目】已知二次函数y=x2﹣4x+5.
(1)将y=x2﹣4x+5化成y=a (x﹣h)2+k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为1,则线段DH长度的最小值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=﹣x+2与反比例函数y=![]() 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y=
的图象有唯一公共点,若直线y=﹣x+b与反比例函数y=![]() 的图象有2个公共点,则b的取值范围是( )
的图象有2个公共点,则b的取值范围是( )

A. b>2 B. ﹣2<b<2 C. b>2或b<﹣2 D. b<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只用无刻度的直尺作图(保留作图痕迹,不要求写作法)
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,其中四边形AEBF是平行四边形,请你在图中画出∠AOB的平分线.
(2)如图2,已知E是菱形ABCD中AB边上的中点,请你在图中画出一个矩形EFGH,使得其面积等于菱形ABCD的一半.

查看答案和解析>>
科目:初中数学 来源: 题型:
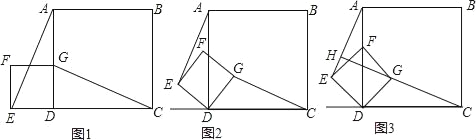
【题目】(1)如图1,正方形ABCD和正方形DEFG,G在AD边上,E在CD的延长线上.求证:AE=CG,AE⊥CG;
(2)如图2,若将图1中的正方形DEFG绕点D顺时针旋转角度θ(0°<θ<90°),此时AE=CG还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,当正方形DEFG绕点D顺时针旋转45°时,延长CG交AE于点H,当AD=4,DG=![]() 时,求线段CH的长.
时,求线段CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=![]() S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
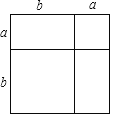
【题目】如图所示的大正方形是由两个小正方形和两个长方形组成.
(1)通过两种不同的方法计算大正方形的面积,可以得到一个数学等式;
(2)利用(1)中得到的结论,解决下面的问题:若a+b=2,ab=﹣3,
求:①a2+b2;
②a4+b4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何探究题
(1)发现:在平面内,若BC=a,AC=b,其中a>b.
当点A在线段BC上时(如图1),线段AB的长取得最小值,最小值为 ;
当点A在线段BC延长线上时(如图2),线段AB的长取得最大值,最大值为 .
(2)应用:点A为线段BC外一动点,如图3,分别以AB、AC为边,作等边△ABD和等边△ACE,连接CD、BE.
①证明:CD=BE;
②若BC=3,AC=1,则线段CD长度的最大值为 .
(3)拓展:如图4,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com