
����Ŀ����ͼ1����������ABCD�У���PΪAD�ӳ�����һ�㣬����AC��CP������C��CF��CP�ڵ�C����AB�ڵ�F������B��BM��CF�ڵ�N����AC�ڵ�M��
��1����![]() ��
�� ![]() ����
����![]() ��
��
��2����![]() ����֤��
����֤�� ![]() ��
��
��3����ͼ2���������������������£�����������ABCD����Ϊ������ABCD������ AB��BC��AC=AP��ȡCP�е�E������EB����AC�ڵ�O�����룺��AOB���ABM֮���к�������ϵ����˵�����ɣ�

���𰸡���1��![]() ����2��֤������������3��֤��������.
����2��֤������������3��֤��������.
�������������������1���������ε����ʵó�AB=BC=CD=5��ADC=��CDP=��ABC=��BCD=90�����ɹ��ɶ������AC���ó�AP���������S��ACP����2����CF�Ͻ�ȡNG=FN������BG����CF-CG=2FN��֤����BCF=��DCP����ASA֤����BCF�ա�DCP���ó�CF=CP��֤��CG=BM����SAS֤����ABM�ա�BCG���ó���AMB=��BGC����ˡ�BMC=��BGF�����߶δ�ֱƽ���ߵ����ʵó�BF=BG���ó���BFG=��BGF����ˡ�BMC=��CBM�����ɵó����ۣ���3������AE����֤����BCA=2��PAE����֤����A��D��E��C�ĵ㹲Բ����Բ�ܽǶ����ó���DCP=��PAE���ó���BCF=��PAE��֤����BCA=2��ABM��Ȼ���������ε�������ʼ��ɵó����ۣ�
�����������AD��BC,AB=BC=CD=5,��ADC=��CDP=��ABC=��BCD=90��
��AC=![]() =
=![]() ��
��
��AP=![]() AC=
AC=![]() ��
��![]() =
=![]() ��
��
��S��ACP=![]() AP��CD=
AP��CD=![]() ��
��![]() ��5=
��5=![]() ;
;
(2)֤������CF�Ͻ�ȡNG=FN������BG����ͼ1��ʾ��

��CFCG=2FN��
��CF��CP��
���PCF=90����
���BCF=��DCP��
����BCF����DCP��,  ��
��
����BCF����DCP(ASA)��
��CF=CP��
��CPBM=2FN��
��CG=BM��
�ߡ�ABC=90����BM��CF��
���ABM=��BCG����BFG=��CBM��
����ABM����BCG��,  ��
��
����ABM����BCG(SAS)��
���AMB=��BGC��
���BMC=��BGF��
��GN=FN��BM��CF��
��BF=BG��
���BFG=��BGF��
���BMC=��CBM��
��BC=MC��
(3)��AOB=3��ABM���������£�
����AE���ӳ�����BC���ӳ����ڵ�G����ͼ2��ʾ��

��AC=AP��E��CP���е㣬
��AE��CP��PE=CE����PAE=��CAE��
��AD��BC��
���BCA=��PAC=2��PAE����PAE=��G��
����APE����GCE��
��AE=GE��
��CP��AG�Ĵ�ֱƽ���ߣ�
��BE=GE��
���G=��CBE��
��CF��CP��
��AG��FC��
���G=��BCF��
�ߡ�PCF=90��,��BCD=90����
���BCF=��DCP��
���CBE=��BCF��
�ߡ�ABM+��BFC=90��,��BCF+��BFC=90����
���ABM=��BCF��
���CBE=��ABM.
�ߡ�DCP+��P=90��,��PAE+��P=90����
���DCP=��PAE��
���BCF=��PAE��
���ABM=��BCF=��PAE��
���BCA=2��ABM��
�ߡ�AOB=��CBE+��BCA��
���AOB=3��ABM.


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȥ���ţ�����a��b+c������������
A. ��a+b+cB. ��a+b��cC. ��a��b+cD. ��a��b��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��ABC��ֱ��MN����������A��B��C��ʹ��A��B��C����ABC����ֱ��MN�Գ�������Ҫ��д������ֻ������ͼ�ۼ���
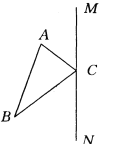
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ж���ʽ���зֽ���ʽ��
��1����x��y��2+16��y��x����
��2��1��a2��b2��2ab��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и���ͼ��һ�����Ƶ��ǣ� ��
A.����ֱ��������B.�����ȱ�������C.��������D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж��ı���ABCDΪƽ���ı��ε��ǣ���������
A.AB��CD��AD��BC
B.OA=OC��OB=OD
C.AD=BC��AB��CD
D.AB=CD��AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ�ڴ�������ɫУ���Ļ�У�����У�İ�ѧ��������������AB�������ڽ�ѧ¥�Ķ�������ͼ��ʾ����С���ڲٳ��ϵĵ�D������1m�ߵIJ����CD���ӵ�C��������Ƶĵײ�B������Ϊ37��Ȼ�����ѧ¥����������4�����F�����ִӵ�E��������ƶ���A����Ϊ45.��֪��ѧ¥��BM=17�ף��ҵ�A��B��M��ͬһֱ���ϣ���������AB�߶ȣ������ȷ��0.1�ס��ο����ݣ�![]() ��sin37��0.60,cos37��0.81,tan37��0.75).
��sin37��0.60,cos37��0.81,tan37��0.75).

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��С�����壬�������ÿ����ֱ����1��2��3��4��5��6���������֣������мס�����λͬѧ����Ϸ����Ϸ�����ǣ����������������������ϵ�������6������ʤ���ߣ�������ϵ����ֲ���6������ʤ���ߣ�����Ϊ�����Ϸ����Լס���˫����ƽ��Ϊʲô���������ƽ������������IJ���ʹ��Ϸ����Լס���˫����ƽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com