
【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证: 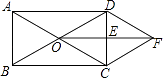
(1)OD=CF;
(2)四边形ODFC是菱形.
科目:初中数学 来源: 题型:
【题目】据报道,2014中国军费预算比上年上涨了12.2%,而美国军费预算比上年下降了1.2%,比较两国军费预算( )
A.中国军费多
B.美国军费多
C.两国一样多
D.条件不足,不能判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm2
(1)求y与x之间的关系式.
(2)求当边长增加多少时,面积增加8 cm2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点C为线段AB上一点,AB=12,AC=8,点D为直线AB上一点,M、N分别是AB、CD的中点,若MN=10,则线段AD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年(2)班的同学在募捐活动中,自愿捐款如下:
每人捐款数(元) | 2 | 5 | 10 | 20 |
相应人数 | 5 | 10 | 20 | 15 |
根据表中给的信息回答下列问题:
(1)该班有多少名学生?
(2)全班共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器按成本价提高30%后标价,再打八折销售,售价为2080元.设该电器的成本价为x元,由题意,下面所列方程正确的是( )
A.80%(1+30%)x=2080
B.30%80%x=2080
C.2080×30%×80%=x
D.30%x=2080×80%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形. 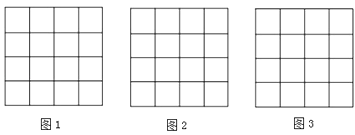
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图3中,画一个正方形,使它的面积是10.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com