
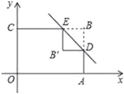
【题目】如图,矩形![]() 的边
的边![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() 。点
。点![]() 分别在
分别在![]() 边上,
边上,![]() 。沿直线
。沿直线![]() 将
将![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处。则点
处。则点![]() 的坐标为__________。
的坐标为__________。
科目:初中数学 来源: 题型:
【题目】在下面给出的数轴中A表示1,B表示﹣2.5,回答下面的问题:
(1)A、B之间的距离是
(2)观察数轴,与点A的距离为5的点表示的数是: ;
(3)若将数轴折叠,使A点与﹣2表示的点重合,则B与数 表示的点重合
(4)若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
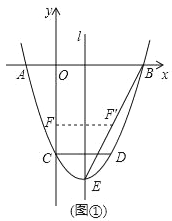
【题目】如图,二次函数y=x2+bx+c的图象与x轴交于 A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;
(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
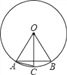
A. 弦AB的长等于圆内接正六边形的边长
B. 弦AC的长等于圆内接正十二边形的边长
C. ![]()
D. ∠BAC=30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方式如图所示,请根据图象回答问题.
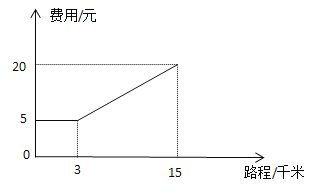
(1)出租车起价是多少元?在多少千米之内只收起价费?
(2)由图象求出起价里程走完之后每行驶1千米所增加的费用;
(3)小张想用30元坐车在该市游玩,试求他最多能走多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一个正比例函数与一个一次函数的图象交于点A(1,4)且一次函数的图象与x轴交于点B(3,0),坐标原点为O.
(1)求正比例函数与一次函数的解析式;
(2)若一次函数交与y轴于点C,求△ACO的面积.
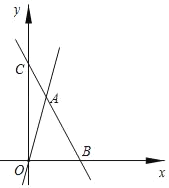
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,得到一个边长为
,得到一个边长为![]() 的正方形.在图1的基础上,某同学设计了一个解释验证
的正方形.在图1的基础上,某同学设计了一个解释验证![]() 的方案(详见方案1)
的方案(详见方案1)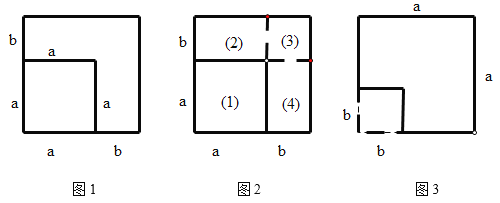
方案1.如图2,用两种不同的方式表示边长为![]() 的正方形的面积.
的正方形的面积.
方式1:![]()
方式2:![]()
因此,![]()
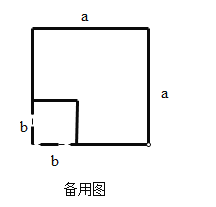
(1)请模仿方案1,在图1的基础上再设计一种方案,用以解释验证![]() ;
;
(2)如图3,在边长为![]() 的正方形纸片上剪掉边长为
的正方形纸片上剪掉边长为![]() 的正方形,请在此基础上再设计一个方案用以解释验证
的正方形,请在此基础上再设计一个方案用以解释验证![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com