
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() ,点
,点![]() 在
在![]() 的半径
的半径![]() 上运动,
上运动,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() 为
为![]() 的切线,切点为
的切线,切点为![]() .
.
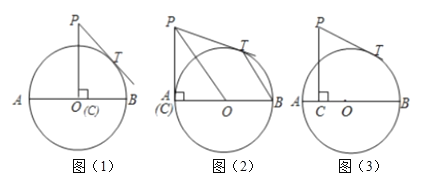
(1)如图(1),当![]() 点运动到
点运动到![]() 点时,求
点时,求![]() 的长;
的长;
(2)如图(2),当![]() 点运动到
点运动到![]() 点时,连接
点时,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(3)如图(3),设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式及
的函数关系式及![]() 的最小值.
的最小值.
科目:初中数学 来源: 题型:
【题目】富贵竹茎叶肥厚,观赏价值高,又有“花开富贵,竹报平安,大吉大利”之意,深受广大花友的喜爱.某花店抓住这个商机,第一次购进![]() 、
、![]() 两种造型的富贵竹共300株.
两种造型的富贵竹共300株.![]() 型富贵竹每盆成本4元,售价8元;
型富贵竹每盆成本4元,售价8元;![]() 型富贵竹每盆成本7元,售价10元.
型富贵竹每盆成本7元,售价10元.
(1)如果第一次购进富贵竹的金额为1500元,那么![]() 型富贵竹购进了多少盆?
型富贵竹购进了多少盆?
(2)富贵竹开始售卖后,十分抢手,花店决定第二次购进这两种造型的富贵竹,它们的进价不变.![]() 型富贵竹的进货量在第一次进货量的基础上增加了
型富贵竹的进货量在第一次进货量的基础上增加了![]() ,售价提高了
,售价提高了![]() ;
;![]() 型富贵竹的售价和进货量不变.结果第二次共获利2100元.求
型富贵竹的售价和进货量不变.结果第二次共获利2100元.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .
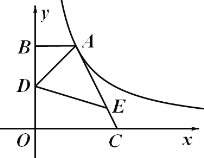
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过
经过![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为第一象限抛物线上一动点,
为第一象限抛物线上一动点,
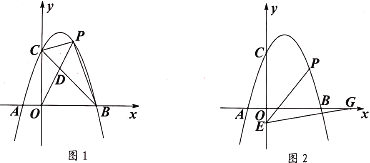
(1)求抛物线的解析式;
(2)如图1,连接![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(3)如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,连接
,连接![]() ,是否存在点
,是否存在点![]() ,使
,使![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点M从点B出发沿线段
,动点M从点B出发沿线段![]() 以每秒2个单位长度的速度向终点C运动;动点N同时从点C出发沿线段
以每秒2个单位长度的速度向终点C运动;动点N同时从点C出发沿线段![]() 以每秒1个单位长度的速度向终点D运动,设运动的时间为
以每秒1个单位长度的速度向终点D运动,设运动的时间为![]() .
.
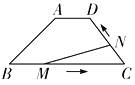
(1)求![]() 的长.
的长.
(2)当![]() 时,求t的值
时,求t的值
(3)试探究:t为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面![]() m,则水流落地点B离墙的距离OB是( )
m,则水流落地点B离墙的距离OB是( )
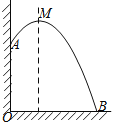
A.2mB.3mC.4mD.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司计划到某绿色蔬菜基地收购A,B两种蔬菜共140吨,预计两种蔬菜销售后获利的情况如下表所示:
销售品种 | A种蔬菜 | B种蔬菜 |
每吨获利(元) | 1200 | 1000 |
其中A种蔬菜的5%,B种蔬菜的3%须运往C市场销售,但C市场的销售总量不超过5.8吨.设销售利润为W元(不计损耗),购进A种蔬菜x吨.
(1)求W与x之间的函数关系式;
(2)将这140吨蔬菜全部销售完,最多可获得多少利润?
(3)由于受市场因素影响,公司进货时调查发现,A种蔬菜每吨可多获利100元,B种蔬菜每吨可多获利m(200<m<400)元,但B种蔬菜销售数量不超过90吨.公司设计了一种获利最大的进货方案,销售完后可获利179000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某飞机场东西方向的地面 l 上有一长为 1km 的飞机跑道 MN(如图),在跑道 MN的正西端 14.5 千米处有一观察站 A.某时刻测得一架匀速直线降落的飞机位于点 A 的北偏西30°,且与点 A 相距 15 千米的 B 处;经过 1 分钟,又测得该飞机位于点 A 的北偏东 60°,且与点 A 相距 5![]() 千米的 C 处.
千米的 C 处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道 MN 之间?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com