
 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源:2017届广东省广州市海珠区九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,一次函数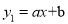 (
( ≠ 0)的图象与
≠ 0)的图象与 轴相交于点A,与反比例函数
轴相交于点A,与反比例函数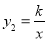 (
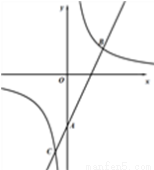
( ≠0)的图象相交于点B(3,2)、C(-1,n).
≠0)的图象相交于点B(3,2)、C(-1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出 >
> 时
时 的取值范围;
的取值范围;
(3)在 轴上是否存在点P,使△PAB为直角三角形,如果存在,请求点P的坐标,若不存在,请说明理由.
轴上是否存在点P,使△PAB为直角三角形,如果存在,请求点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017届浙江省嘉兴市十校九年级下学期4月联合模拟数学试卷(解析版) 题型:单选题
如图,∠AOB的一边OA为平面镜,∠AOB=38°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )

A. 76° B. 52° C. 45° D. 38°
查看答案和解析>>
科目:初中数学 来源:2017届山东省济南市历下区九年级3月模拟考试数学试卷(解析版) 题型:单选题
我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2015年这两年的平均增长率为x,则下列方程正确的是( )
A. 1.4(1+x)=4.5
B. 1.4(1+2x)=4.5
C. 1.4(1+x)2=4.5
D. 1.4(1+x)+1.4(1+x)2=4.5
查看答案和解析>>
科目:初中数学 来源:2017届安徽合肥市九年级中考模拟数学试卷(解析版) 题型:解答题
【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源:2017届山东省济南市区九年级学业水平考试第二次模拟考试数学试卷(解析版) 题型:解答题
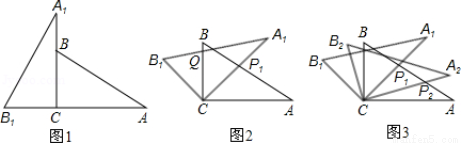
将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图2中,若AP1=a,则CQ等于多少?
(3)将图2中△A1B1C绕点C顺时针旋转到△A2B2C(如图3),点P2是A2C与AP1的交点.当旋转角为多少度时,有△AP1C∽△CP1P2?这时线段CP1与P1P2之间存在一个怎样的数量关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com