
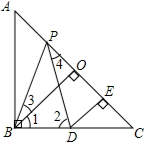
 如图,已知在Rt△ABC中,AB=AC,∠ABC=90°,BO⊥AC于点O,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E;
如图,已知在Rt△ABC中,AB=AC,∠ABC=90°,BO⊥AC于点O,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E;分析 (1)根据等腰三角形的性质和三角形外角的性质可得到∠2=∠1+∠3=∠4+∠C,可得到∠3=∠4,可证明△BPO≌△PDE;
(2)由角平分线的定义结合(1)可证得∠ABP=∠4,结合条件可证明△ABP≌△CPD,可证得AP=CD.
解答 证明:
(1)∵PB=PD,
∴∠2=∠1+∠3,且∠2=∠C+∠4,
∵AB=AC,∠ABC=90°,BO⊥AC,
∴∠1=∠C=45°,
∴∠3=∠4,
在△BPO和△PDE中
$\left\{\begin{array}{l}{∠3=∠4}\\{∠POB=∠PED=90°}\\{PB=PD}\end{array}\right.$
∴△BPO≌△PDE(AAS);
(2)∵PB平分∠ABO,
∴∠3=∠ABP,
由(1)可知∠3=∠4,
∴∠ABP=∠4,
在△ABP和△CPD中
$\left\{\begin{array}{l}{∠A=∠C}\\{AB=CP}\\{∠ABP=∠4}\end{array}\right.$
∴△ABP≌△CPD(ASA),
∴AP=CD.
点评 本题主要考查全等三角形的判定和性质,在(1)中注意等腰三角形性质的应用,在(2)中注意角平分线的应用.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{2800}{x}$-$\frac{2800}{5x}$=2 | B. | $\frac{2800}{5x}$-$\frac{2800}{x}$=2 | C. | $\frac{2800}{x}$-$\frac{2800}{4x}$=2 | D. | $\frac{2800}{4x}$-$\frac{2800}{x}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(m3) | 收费(元) |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
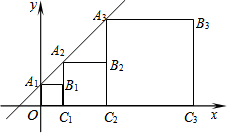 如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,AnBnCnCn-1按所示的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B2015的坐标是(22015-1,22014).
如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,AnBnCnCn-1按所示的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B2015的坐标是(22015-1,22014).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.
小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成本(元/个) | 售价 (元/个) | |
| A | 2 | 2.4 |
| B | 3 | 3.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2,3 | B. | 32,42,52 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
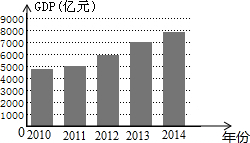 如图是表示某地区 2010~2014年生产总值(简称GDP,单位:亿元)的统计图,根据统计图所提供的信息,判断下列说法正确的是( )
如图是表示某地区 2010~2014年生产总值(简称GDP,单位:亿元)的统计图,根据统计图所提供的信息,判断下列说法正确的是( )| A. | 2012年该地区的GDP未达到5500亿元 | |
| B. | 2014年该地区的GDP比2012年翻一番 | |
| C. | 2012~2014年该地区每年GDP增长率相同 | |
| D. | 2012~2014年该地区的GDP逐年增长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com