
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E. 
(1)求证:△BEF∽△DBC.;
(2)若⊙O的半径为3,∠C=32°,求BE的长.(精确到0.01)
【答案】
(1)证明:连接OB.
∵过点B的切线AE与CD的延长线交于点A,
∴OB⊥AE,
∴∠OBE=∠EBF+∠CBO=90°.
∵CD为⊙O的直径
∴∠CBD=∠CBO+∠OBD=90°,
∴∠EBF=∠OBD.
∵OB、OD是⊙O的半径,
∴OB=OD,
∴∠OBD=∠CDB,
∴∠EBF=∠CDB.
∵OE∥BD,
∴∠EFB=∠CBD
∴△BEF∽△DBC
(2)解:∵由(1)可知△BEF∽△DBC
∴∠OBE=90°,
∴∠E=∠C.
∵∠C=32°,
∴∠E=∠C=32°.
∵⊙O的半径为3,
∴OB=3.
在Rt△BOE中,∠OBE=90°,∠E=32°,OB=3,
∴tanE= ![]() ,即tan32°=
,即tan32°= ![]() ,
,
∴BE= ![]() ≈4.80.
≈4.80.

【解析】(1)连接OB,由切线的性质得出OB⊥AE,故可得出∠OBE=∠EBF+∠CBO=90°.再由圆周角定理得出∠CBD=∠CBO+∠OBD=90°,故∠EBF=∠OBD.根据等腰三角形的性质可知∠OBD=∠CDB,故∠EBF=∠CDB,进而可得出结论;(2)由(1)可知△BEF∽△DBC,所以∠OBE=90°,∠E=∠C.在Rt△BOE中,利用锐角三角函数的定义即可得出结论.
【考点精析】掌握切线的性质定理和相似三角形的判定与性质是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB上有两点C、D,且AC=BD,M、N分别是线段AC 、AD的中点,若AB=a cm ,AC=BD=b cm,且a,b满足(a-9)2+|b-7 |=0.
![]()
(1)求AB ,AC的长度;
(2)求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.

查看答案和解析>>
科目:初中数学 来源: 题型:
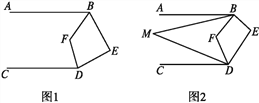
【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6![]() 的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
①∠CBH=45°;②点H是EG的中点;③EG=4![]() ;④DG=2
;④DG=2![]() .
.
其中,正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E. 
(1)求证:△BEF∽△DBC.;
(2)若⊙O的半径为3,∠C=32°,求BE的长.(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是A.B两所学校艺术节期间收到的各类艺术作品情况的统计图:


A学校 B学校
(1)从图中你能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺木作品的总数分别是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是以O为圆心,AB为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的斜边和直角边所在的直线与直径AB分别相交于C,D两点.设线段AD的长为x,线段BC的长为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com