
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到![]() 、
、![]() 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往
两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往![]() 、
、![]() 两城镇的运费分别为每辆800元和900元,用小货车运往
两城镇的运费分别为每辆800元和900元,用小货车运往![]() 、
、![]() 两城镇的运费分别为每辆400元和600元.
两城镇的运费分别为每辆400元和600元.
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往![]() 城镇,其余货车前往
城镇,其余货车前往![]() 城镇,设前往
城镇,设前往![]() 城镇的大货车为
城镇的大货车为![]() 辆,前往
辆,前往![]() 、
、![]() 两城镇总费用为
两城镇总费用为![]() 元,试求出
元,试求出![]() 与
与![]() 的函数解析式.若运往
的函数解析式.若运往![]() 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
【答案】(1) 大货车用8辆,小货车用7辆;(2) ![]() 与
与![]() 的函数解析式为y=100x+9400;当运往
的函数解析式为y=100x+9400;当运往![]() 城镇的防护用品不能少于100箱,最低费用为9900元.
城镇的防护用品不能少于100箱,最低费用为9900元.
【解析】
(1)设大货车用x辆,小货车用y辆,然后根据题意列出二元一次方程组并求解即可;
(2)设前往A城镇的大货车为x辆,则前往B城镇的大货车为(8-x)辆,前往A城镇的小货车为(10-x)辆,前往B城镇的小货车为[7-(10-x)]辆,然后根据题意即可确定y与x的函数关系式;再结合已知条件确定x的取值范围,求出总费用的最小值即可.
解:(1)设大货车用x辆,小货车用y辆,根据题意得:
![]()
解得:![]()
答:大货车用8辆,小货车用7辆;
(2)设前往A城镇的大货车为x辆,则前往B城镇的大货车为(8-x)辆,前往A城镇的小货车为(10-x)辆,前往B城镇的小货车为[7-(10-x)]辆,
根据题意得:y=800x+900(8-x)+400(10-x)+600[7-(10-x)]=100x+9400
由运往![]() 城镇的防护用品不能少于100箱,则12x+ 8 (10-x)≥100,解得x≥5且x为整数;
城镇的防护用品不能少于100箱,则12x+ 8 (10-x)≥100,解得x≥5且x为整数;
当x=5时,费用最低,则:100×5+9400=9900元.
答:![]() 与
与![]() 的函数解析式为y=100x+9400;当运往
的函数解析式为y=100x+9400;当运往![]() 城镇的防护用品不能少于100箱,最低费用为9900元.
城镇的防护用品不能少于100箱,最低费用为9900元.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,P,Q分别在AB,BC的延长线上,BP=CQ,连接AQ,DP交于点O,并分别与CD,BC交于点F,E,连接AE.下列结论:
①AQ⊥DP
②OA2=OEOP
③S△AOD=S四边形OECF
④当BP=1时,tan∠OAE=![]()
其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某口罩加工厂有![]() 两组工人共
两组工人共![]() 人,
人,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 两组工人每小时一共可加工口罩
两组工人每小时一共可加工口罩![]() 只.
只.
(1)求![]() 两组工人各多少人;
两组工人各多少人;
(2)由于疫情加重![]() 两组工人均提高了工作效率,一名
两组工人均提高了工作效率,一名![]() 组工人和一名
组工人和一名![]() 组工人每小时共可生产口罩
组工人每小时共可生产口罩![]() 只,若
只,若![]() 两组工人每小时至少加工
两组工人每小时至少加工![]() 只口罩,那么
只口罩,那么![]() 组工人每人每小时至少加工多少只口罩?
组工人每人每小时至少加工多少只口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
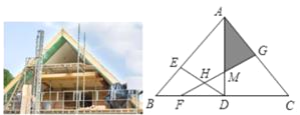
【题目】工人师傅在修茸一人字架屋顶BAC时需要加固,计划焊接三根钢条AD,DE,FG.在如图所示的△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E,F,G分别是AB,BD,AC上的点,连接DE,GF,交于点H,GF与AD交于点M,当H为FM的中点,BF∶CF=1∶5,AG:AE=5:7时,△AGM的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
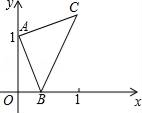
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.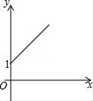 B.
B.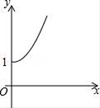
C.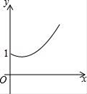 D.
D.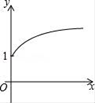
查看答案和解析>>
科目:初中数学 来源: 题型:
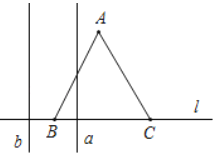
【题目】如图,边长为![]() 的正
的正![]() 的边
的边![]() 在直线
在直线![]() 上,两条距离为
上,两条距离为![]() 的平行直线
的平行直线![]() 和
和![]() 垂直于直线
垂直于直线![]() ,
,![]() 和
和![]() 同时向右移动(
同时向右移动(![]() 的起始位置在
的起始位置在![]() 点),速度均为每秒
点),速度均为每秒![]() 个单位,运动时间为
个单位,运动时间为![]() (秒),直到
(秒),直到![]() 到达
到达![]() 点停止,在
点停止,在![]() 和
和![]() 向右移动的过程中,记
向右移动的过程中,记![]() 夹在
夹在![]() 和
和![]() 间的部分的面积为
间的部分的面积为![]() ,则
,则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.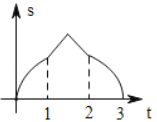 B.
B.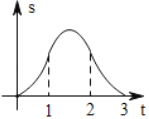
C.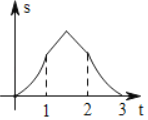 D.
D.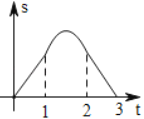
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现:如图①,点A为一动点,点B和点C为两个定点,且![]() ,
,![]() (
(![]() ).
).
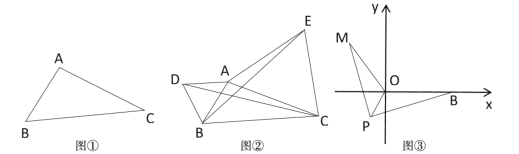
填空:当点![]() 位于_______时,线段
位于_______时,线段![]() 的长取得最小值,且最小值为_______(用含
的长取得最小值,且最小值为_______(用含![]() 的式子表示);
的式子表示);
(2)如图②应用:点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,如图2分别以
,如图2分别以![]() 、
、![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 、
、![]() .
.
①请找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最小值.
长的最小值.
(3)拓展:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段OB外一动点,且
为线段OB外一动点,且![]() ,
,![]() ,
,![]() ,请求出
,请求出![]() 的最小值并直接写出点
的最小值并直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
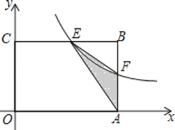
(1)当F为AB的中点时,求该反比例函数的解析式和点E的坐标.
(2)设过(1)中的直线EF的解析式为y=ax+b,直接写出不等式ax+b<![]() 的解集.
的解集.
(3)当k为何值时,△AEF的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
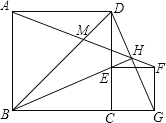
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com